题目内容
【题目】如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.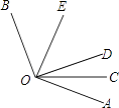
(1)如果∠AOB=150°,求∠COE的度数;
(2)如果∠AOB=120°,那么∠COE=;
(3)如果∠AOB=α,那么∠COE= .
【答案】
(1)解:∵OC是∠AOD的平分线,
∴∠COD= ![]() ∠AOD,
∠AOD,
∵OE是∠BOD的平分线,
∴∠EOD= ![]() ∠BOD,
∠BOD,
∴∠COE=∠EOD+∠COD= ![]() ∠AOD+
∠AOD+ ![]() ∠BOD=
∠BOD= ![]() (∠BOD+∠AOD)=
(∠BOD+∠AOD)= ![]() ∠BOA,
∠BOA,
∵∠AOB=150°,
∴∠EOC=75°
(2)60°
(3)![]()
【解析】解:(2)∵∠COE= ![]() ∠AOB,∠AOB=120°,
∠AOB,∠AOB=120°,
∴∠COE=60°,
所以答案是:60°;
⑵∵∠COE= ![]() ∠AOB,∠AOB=α,
∠AOB,∠AOB=α,
∴∠COE= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握角的运算(角之间可以进行加减运算;一个角可以用其他角的和或差来表示)的相关知识才是答题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目