题目内容
【题目】由若干边长为1的小正方形拼成一系列“L”形图案(如图1).
(1)当“L”形由7个正方形组成时,其周长为;
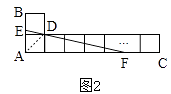
(2)如图2,过格点D作直线EF,分别交AB,AC于点E,F.
①试说明AEAF=AE+AF;
②若“L”形由n个正方形组成时,EF将“L”形分割开,直线上方的面积为整个“L”形面积的一半,试求n的取值范围以及此时线段EF的长.
【答案】
(1)16
(2)
解:①如图2中,连接AD,
∵S△EAF=S△ADE+S△ADF= ![]() AEAF=
AEAF= ![]() AE1+
AE1+ ![]() AF1,
AF1,
∴AEAF=AE+AF.
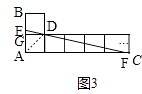
②如图3中,设有n个正方形,AE=x,AF=y,
∵ ![]() xy=
xy= ![]() n,
n,
∴xy=x+y=n,
∴x=n﹣y ①
∵DG∥AF,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴xy﹣y=x ②
①代入②得到,y2﹣ny+n=0,
∵△≥0,
∴n2﹣4n≥0,
解得n≤0或n≥4,
∵n>0,
∴n≥4.
∴EF= ![]() =
= ![]() =
= ![]()
【解析】解:(1)当“L”形由7个正方形组成时,其周长为2×7+2=16.
所以答案是16.
【考点精析】解答此题的关键在于理解两点间的距离的相关知识,掌握同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目