题目内容
【题目】（本题满分8分）如图，四边形ABCD中，
,E是边CD的中点，连接BE并延长与AD的延长线相较于点F．
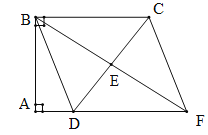
（1）求证：四边形BDFC是平行四边形；
（2）若△BCD是等腰三角形，求四边形BDFC的面积．
【答案】（1）见解析；（2）6
或
【解析】
试题（1）根据平行线的性质和中点的性质证明三角形全等，然后根据对角线互相平分的四边形是平行四边形完成证明；
（2）由等腰三角形的性质，分三种情况：①BD=BC,②BD=CD,③BC=CD,分别求四边形的面积．
试题解析：（1）证明：∵∠A=∠ABC=90°
∴AF∥BC
∴∠CBE=∠DFE,∠BCE=∠FDE
∵E是边CD的中点
∴CE=DE
∴△BCE≌△FDE（AAS）
∴BE=EF
∴四边形BDFC是平行四边形
（2）若△BCD是等腰三角形
①若BD=DC
在Rt△ABD中，AB=
∴四边形BDFC的面积为S=
×3=6；
②若BD=DC
过D作BC的垂线，则垂足为BC得中点，不可能；
③若BC=DC
过D作DG⊥BC,垂足为G
在Rt△CDG中，DG=
∴四边形BDFC的面积为S=．
练习册系列答案
全能测控期末小状元系列答案
相关题目
