Question

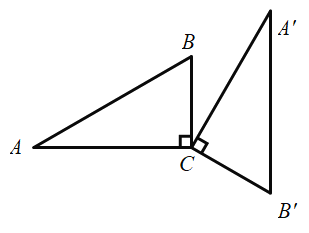
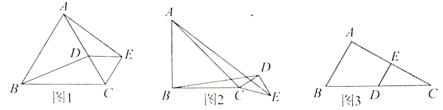
【题目】问题发现：（1）如图1，与同为等边三角形，连接则与的数量关系为________；直线与所夹的锐角为_________；

类比探究：（2）与同为等腰直角三角形，其他条件同（1），请问（1）中的结论还成立吗？请说明理由；

拓展延伸：（3）中，为的中位线，将绕点逆时针自由旋转，已知，在自由旋转过程中，当在一条直线上时，请直接写出的值．

Answer 1

【答案】（1），；（2）不成立，见解析；（3）2或4

【解析】

（1）根据题意，利用等边三角形的性质，得出，再根据全等三角形对应角相等，得出，故得出与所夹的锐角为60°．

（2）根据题意，利用等腰直角三角形的性质可推出，再根据相似三角形对应角相等，得出，故得出直线与所夹的锐角为45°，与（1）结论不符．

（3）此问需要分两种情况讨论，一种情况是当在直线上，该种情况需要先证明，从而根据相似三角形的性质得到，最后根据全等三角形的性质求出；另一种情况是，当在直线下，先证明，从而证明四边形为矩形，最后求出．

解：（1）；60°

解答如下：如图１，

与为等边三角形，

，

在与中，

，

故答案为：；直线与所夹的锐角为60°．

（2）不成立

理由如下：与为等腰直角三角形，

，，

，

即：，

在与中，

故（1）中的结论不成立；

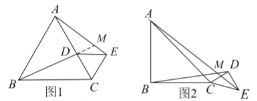
（3）的长度为2或4；

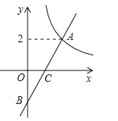
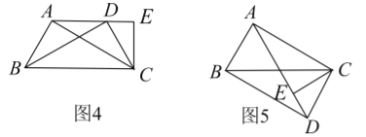
①点在直线上方时如图4，

，

，

②点在直线下方时，如图5，

∥

根据题意，易证四边形为矩形，

，

故答案为

综上可得的长度为2或4