题目内容
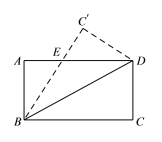
【题目】如图 1,在平面直角坐标系中,A,B,D 三点的坐标是(0,2),(-2,0),(1,0),点C 是 x 轴下方一点,且 CD⊥AD,∠BAD+∠BCD=180°,AD=CD
(1)求证:BD 平分∠ABC
(2)求四边形 ABCD 的面积
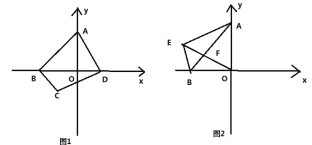
(3)如图 2,BE 是∠ABO 的邻补角的平分线,连接 AE,OE 交 AB 于点 F,若∠AEO=45°,求证:AF=AO.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析;
;(3)证明见解析;
【解析】
(1)过C作DM⊥BD于M,根据AAS判定△CDM≌△DOA,通过线段和差推出BM=MC=1得出∠CBD=45°进而得到∠CBD=∠ABO=45°即可证BD 平分∠ABC;
(2)将![]() ,再根据三角形的面积公式计算即可;
,再根据三角形的面积公式计算即可;
(3)过点E作作EH⊥x轴于点H,EG⊥BC于点G,根据角平分线的性质得到EH=EG,证明△EAG≌△EOH,得到EA=EO,根据等腰三角形的判定定理解答.
证明:(1)∵A(0,2)B(-2,0)D(1,0)
∴OA=OB=2,OD=1
∴∠ABO=∠BAO=45°
过C作DM⊥BD于M
∴∠CMD=90°
∴∠1+∠3=90°
∵CD⊥AD
∴∠ADC=90°
∴∠1+∠2=90°
∴∠2=∠3
又∵CD=AD,∠CMD=∠AOD =90°
∴△CDM≌△DOA
∴CM=OD=1,MD=AO=2
∴OM=1
∴BM=1
∴BM=MC=1
∴∠CBD=45°
∴∠CBD=∠ABO=45°
∴BD 平分∠ABC
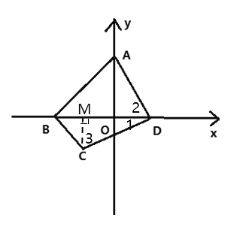
(2)由(1)得A(0,2),B(-2,0),C(-1,-1),M(-1,0)
∴BD=3,AO=2,CM=1
∴![]()
∴![]()
(3)过点E作EH⊥x轴于点H,EG⊥BA于点G,
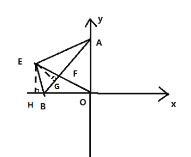
∴∠EHO=∠EGA =90°
∵E点在∠ABO的邻补角的平分线上,EH⊥HO,EG⊥BA
∴EH=EG,
∵∠ABO=∠AEO=45,
∴∠EAG=∠EOH,
在△EAG和EOH中,
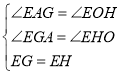
∴△EAG≌△EOH(AAS),
∴EA=EO,
∵∠AEO=45°,
∴∠EAO=∠EOA=67.5°,
∵∠OAB=45°,
∴∠AFO=180°-∠OAB-∠AOE=67.5°
∴∠AOE=∠AFO=67.5°,
∴AF=AO

 发散思维新课堂系列答案
发散思维新课堂系列答案