题目内容
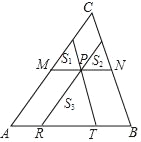
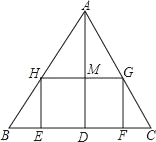
【题目】如图，△ABC是一张锐角三角形的硬纸片．AD是边BC上的高，BC=40cm，AD=30cm．从这张硬纸片剪下一个长HG是宽HE的2倍的矩形EFGH．使它的一边EF在BC上，顶点G，H分别在AC，AB上．AD与HG的交点为M．
（1）求证： 
；
（2）求这个矩形EFGH的周长．
【答案】（1）证明见解析（2）矩形EFGH的周长为72cm
【解析】试题分析：（1）根据矩形性质得出∠AHG=∠ABC，再证明△AHG∽△ABC，即可得出结论；
（2）根据（1）中比例式即可求出HE的长度，以及矩形的周长．
试题解析：（1）证明：∵四边形EFGH为矩形，∴EF∥GH，∴∠AHG=∠ABC，
又∵∠HAG=∠BAC，∴△AHG∽△ABC，∴ 
；
（2）解：由（1）
得：设HE=xcm，则MD=HE=xcm．
∵AD=30cm，∴AM=（30﹣x）cm．∵HG=2HE，∴HG=（2x）cm，可得： 
，
解得：x=12，故HG=2x=24，所以矩形EFGH的周长为：2×（12+24）=72（cm）．
答：矩形EFGH的周长为72cm．
练习册系列答案
相关题目
