��Ŀ����
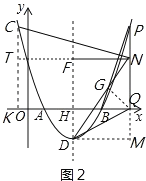
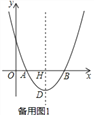
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y=ax2��10ax+16a��a��0����x����A��B���㣬�����ߵĶ���ΪD���Գ�����x�ύ�ڵ�H����AB=2DH��
��1����a��ֵ��
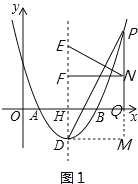
��2����P�ǶԳ����Ҳ��������ϵĵ㣬����PD��PQ��x���ڵ�Q����N���߶�PQ�ϵĵ㣬����N��NF��DH�ڵ�F��NE��PD��ֱ��DH�ڵ�E�����߶�EF�ij���
��3���ڣ�2���������£�����DN��DQ��PB����DN=2QN��NQ��3����2��NDQ+��DNQ=90��ʱ����NC��PB���Գ��������������ڵ�C�����C�����꣮
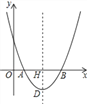
���𰸡���1��![]() ����2��3����3����C����1��9������
����2��3����3����C����1��9������
�������������������1������y=ax2-10ax+16a������õ�y=0ʱ��x��ֵ���Ӷ�������õ�A��B�����꣬�������ߵĶ���ΪD���Գ�����x�ύ�ڵ�H����AB=2DH���Ӷ��������a��ֵ��
��2��������֪����������Ӧ��ͼ�Σ�Ȼ�����������Ŀ�е�������ϵ��ͨ�������ο������EF�ij���
��3������������Ի�����Ӧ��ͼ�Σ�Ȼ�������Ŀ�еĹ�ϵ���������������ƣ����仯������õ�C�����꣮
�����������1����y=0����x=2��x=8�����A��2��0����B��8��0������AB=6��
��AB=2DH����DH=3��
��OH=2+![]() ����D��5����3�����ੁ3=a��52��10a��5+16a����a=
����D��5����3�����ੁ3=a��52��10a��5+16a����a=![]() ��
��
��2����ͼ1������D��PQ�Ĵ��ߣ���PQ���ӳ����ڵ�M��
��NE��PD�����DPN+��PNE=90�㣬��NF��DE�����FEN+��FNE=90�㣬
�֡�DH��x�ᣬPQ��x�ᣬ��DE��PQ�����FEN=��PNE�����DPM=��ENF�����EFN�ס�DMP��
��![]() �����P��t��
�����P��t�� ![]() ������FN=DM=t��5��PM=
������FN=DM=t��5��PM=![]() +3��������EF=3��
+3��������EF=3��
��3����ͼ2����QG��DN�ڵ�G����DF��PQ�����FDN=��DNQ����2��NDQ+��DNQ=90�㣬
��2��NDQ+��FDN=90�㣬�ߡ�FDM=90�㣬���NDM=2��NDQ�����NDQ=��MDQ����QG=QM=DH=3��
��QN=m����DN=2m����sin��DNM=![]() ��sin��QNG=
��sin��QNG=![]() ��sin��DNM=sin��QNG��
��sin��DNM=sin��QNG��
��![]() ����DM=6=DG����OQ=5+6=11��
����DM=6=DG����OQ=5+6=11��
���P���������ǣ� ![]() =9�����P��11��9����
=9�����P��11��9����
��NG=2m��6����Rt��NGQ��QG2+NG2=QN2��
��32+��2m��6��2=m2���ã�m=3���ᣩ��m=5��
��C��n�� ![]() ������CK��x���ڵ�K����NF��CK�ڵ�K����CT=
������CK��x���ڵ�K����NF��CK�ڵ�K����CT=![]() ��NT=11��n��
��NT=11��n��
��P��11��9������BQ=11��8=3��PQ=9��
��CN��PB��PQ��CK��PQ��x�ᣬ ���CTN�ס�BQP��
��![]() �� ��
�� ��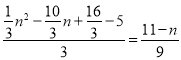 �� ��ã�n=��1��n=10����ȥ����
�� ��ã�n=��1��n=10����ȥ����
���C����1��9����