Question

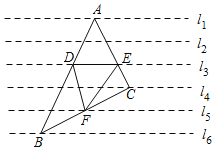
【题目】如图，一组等距的平行线，点A、B、C分别在直线l1、l6、l4上，AB交l3于点D，AC交l3于点E，BC交于l5点F，若△DEF的面积为1，则△ABC的面积为_____．

Answer 1

【答案】

【解析】

在三角形中由同底等高，同底倍高求出，根据平行线分线段成比例定理，求出，最后由三角形的面积的和差法求得．

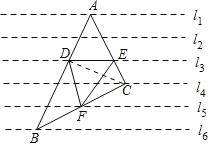
连接DC，设平行线间的距离为h，

AD=2a，如图所示：

∵，

，

∴S△DEF=S△DEA，

又∵S△DEF=1，

∴S△DEA=1，

同理可得：，

又∵S△ADC=S△ADE+S△DEC，

∴，

又∵平行线是一组等距的，AD=2a，

∴，

∴BD=3a，

设C到AB的距离为k，

∴ak，

，

∴，

又∵S△ABC=S△ADC+S△BDC，

∴．

故答案为：．