Question

【题目】如图，二次函数y＝ax2﹣3ax+c的图象与x轴交于点A、B，与y轴交于点C直线y＝﹣x+4经过点B、C．

（1）求抛物线的表达式；

（2）过点A的直线交抛物线于点M，交直线BC于点N．

①点N位于x轴上方时，是否存在这样的点M，使得AM：NM＝5：3？若存在，求出点M的坐标；若不存在，请说明理由．

②连接AC，当直线AM与直线BC的夹角∠ANB等于∠ACB的2倍时，请求出点M的横坐标．

Answer 1

【答案】（1）y＝﹣x2+3x+4；（2）①不存在符合条件的M点,理由见解析；②M．

【解析】

（1）由直线y＝﹣x+4知：点B、C的坐标分别为（4，0）、（0，4），则二次函数表达式为：y＝ax2﹣3ax+4，将点A的坐标代入上式，即可求解；

（2）①设点N（m，mk+k），即：mk+k＝﹣m+4①，则点，将点M的坐标代入二次函数表达式得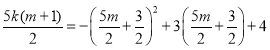：②，联立①②即可求解；②当∠ANB＝2∠ACB时，则∠ANB＝90°，即可求解．

解：（1）由直线y＝﹣x+4知：点B、C的坐标分别为（4，0）、（0，4），

则二次函数表达式为：y＝ax2﹣3ax+4，将点A的坐标代入上式并解得：a＝﹣1，

故抛物线的表达式为：y＝﹣x2+3x+4，

则点A（﹣1，0）；

（2）①存在，理由：

设直线AM的表达式为：y＝kx+b，

将点A的坐标代入上式并解得：

直线AM的表达式为：y＝kx+k，

如图1所示，分别过点M、N作x轴的垂线交于点H、G，

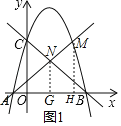
∵AM：NM＝5：3，则MH＝NG，

设点N（m，mk+k），即：mk+k＝﹣m+4…①，

则点，

将点M的坐标代入二次函数表达式得：

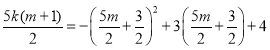②，

联立①②并整理得：5m2﹣2m+3＝0，

△＜0，故方程无解，
故不存在符合条件的M点；

②当∠ANB＝2∠ACB时，如下图，

则∠NAC=∠NCA，、
∴CN=AN，
直线BC的表达式为：y=-x+4
设点N（n，-n+4），
由CN=AN，
即：（n）2+（4-n-4）2=（n+1）2+（4-n）2，
解得：

则点,

将点N、A坐标代入一次函数表达式并解得：
直线NA的表达式为：

将③式与二次函数表达式联立并解得：

故点M