题目内容
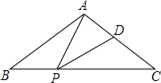
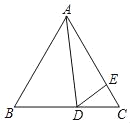
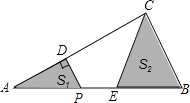
【题目】如图，在△ABC中，∠ACB＝90°，AC＝4，BC＝3，P是AB边上一动点，PD⊥AC于点D，点E在P的右侧，且PE＝1，连接CE，P从点A出发，沿AB方向运动，当E到达点B时，P停止运动，在整个运动过程中，阴影部分面积S1+S2的大小变化的情况是（ ）
A.一直减小B.一直增大
C.先增大后减小D.先减小后增大
【答案】D
【解析】
设PD＝x，AB边上的高为h，分别利用相似三角形的性质和面积法求出AD、h，构建二次函数，再利用二次函数的性质解答即可．
解：在Rt△ABC中，∵∠ACB＝90°，AC＝4，BC＝3，
∴AB＝
＝5，设PD＝x，AB边上的高CF=h，如图，则h＝
，
∵PD∥BC，∴△ADP∽△ACB，
∴
，即
，
∴AD＝
x，PA＝
x，
∴S1+S2＝
xx+（4﹣x）
＝
x2﹣2x+
＝（x﹣
）2+
，
当点E到达点B时，4﹣x=0，解得：
，
∵抛物线的开口向上，对称轴是直线
，
∴当0＜x≤时，S1+S2的值随x的增大而减小，当
时，S1+S2的值随x的增大而增大．
故选：D．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】创客联盟的队员想用3D的打印完成一幅边长为6米的正方形作品ABCD，设计图案如图所示（四周阴影是四个全等的矩形，用材料甲打印；中心区是正方形MNPQ，用材料乙打印）．在打印厚度保持相同的情况下，两种材料的消耗成本如表：
材料 | 甲 | 乙 |
价格（元/米2） | 50 | 40 |
设矩形的较短边AH的长为x米，打印材料的总费用为y元．
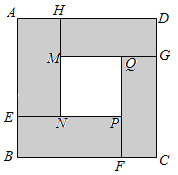
（1）MQ的长为 米（用含x的代数式表示）；
（2）求y关于x的函数解析式；
（3）当中心区的边长不小于2米时，预备资金1700元购买材料一定够用吗？请说明理由．
