题目内容
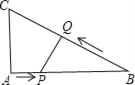
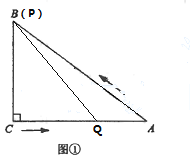
【题目】如图①,在![]() 中,
中,![]() ,
,![]() cm,动点
cm,动点![]() 以2cm/s的速度在
以2cm/s的速度在![]() 的边上沿
的边上沿![]() 的方向匀速运动,动点
的方向匀速运动,动点![]() 在
在![]() 的边上沿
的边上沿![]() 的方向匀速运动,
的方向匀速运动,![]() 、
、![]() 两点同时出发,5s后,点
两点同时出发,5s后,点![]() 到达终点
到达终点![]() ,点
,点![]() 立即停止运动(此时点
立即停止运动(此时点![]() 尚未到达点
尚未到达点![]() ).设点
).设点![]() 运动的时间为
运动的时间为![]() (s),
(s),![]() 的面积为
的面积为![]() (cm2),
(cm2),![]() 与
与![]() 的函数图像如图②所示.
的函数图像如图②所示.
(1)图①中![]() cm,点
cm,点![]() 运动的速度为 cm/s;
运动的速度为 cm/s;
(2)求函数![]() 的最大值;
的最大值;
(3)当![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?请说明理由.
相似?请说明理由.

【答案】(1)AC=8cm,点![]() 运动的速度为5÷5=1cm/s;
运动的速度为5÷5=1cm/s;
(2)当t=4时,函数![]() 的最大值S=
的最大值S=![]()
(3) t=![]() 或t=
或t=![]()
【解析】
(1)由勾股定理求得AC的长,再利用![]() 的面积为9,得
的面积为9,得![]() ,即可解题;(2)过点P作PH⊥AC于H,证明△AHP∽△ACB得
,即可解题;(2)过点P作PH⊥AC于H,证明△AHP∽△ACB得![]() ,求出边长表示S△APQ=
,求出边长表示S△APQ=![]() =
=![]() ,整理成顶点式即可解题;(3)分两种情况讨论当∠PQA=90°时,当∠QPA=90°时,见详解.
,整理成顶点式即可解题;(3)分两种情况讨论当∠PQA=90°时,当∠QPA=90°时,见详解.
解:(1)∵动点![]() 以2cm/s的速度运动了5秒到B点, 如下图,
以2cm/s的速度运动了5秒到B点, 如下图,
∴AB=10cm,
∵![]() ,
,![]() cm,
cm,
∴AC=8cm(勾股定理)
由图2可知当时间为5秒时,![]() 的面积为9,
的面积为9,
即![]() ,
,
∵BC=CP=6,
∴AQ=3,CQ=8-3=5,
∴点![]() 运动的速度为5÷5=1cm/s;
运动的速度为5÷5=1cm/s;
(2)如下图,过点P作PH⊥AC于H,
易证△AHP∽△ACB,
∴![]() ,
,
∴![]() ,解得:PH=
,解得:PH=![]()
∵CQ=t,
∴AQ=8-t,
∴S△APQ=![]() =
=![]() =
=![]()
∴当t=4时,函数![]() 的最大值S=
的最大值S=![]()
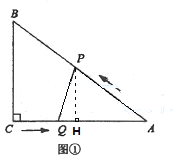
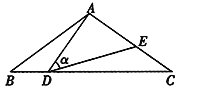
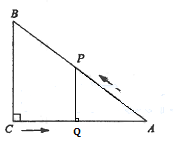
(3)分两种情况,当∠PQA=90°时,如下图,
△AQP∽△ACB,
∴![]() ,
,![]() ,解得:t=
,解得:t=![]() ;
;
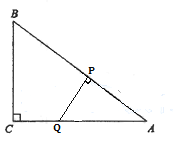
当∠QPA=90°时,如下图,
△AQP∽△ABC,
∴![]() ,
,![]() ,解得:t=
,解得:t=![]() ;
;
综上, t=![]() 或t=
或t=![]() 时以
时以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目