题目内容
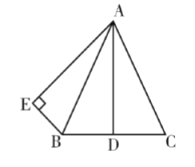
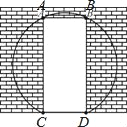
【题目】如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=![]() 米.
米.
(1)求此圆形门洞的半径;
(2)求要打掉墙体的面积.
【答案】 (1)圆形门洞的半径为![]() ;(2)要打掉墙体的面积为(
;(2)要打掉墙体的面积为(![]() π﹣
π﹣![]() )平方米 .
)平方米 .
【解析】
(1)先证得BC是直径,在直角三角形BCD中,由BD与CD的长,利用勾股定理求出BC的长,即可求得半径;
(2)打掉墙体的面积=2(S扇形OAC﹣S△AOC)+S扇形OAB﹣S△AOB,根据扇形的面积和三角形的面积求出即可.
(1)连结AD、BC.
∵∠BDC=90°,∴BC是直径,∴BC=![]() =
=![]() ,∴圆形门洞的半径为
,∴圆形门洞的半径为![]() .
.
(2)取圆心O,连结OA.由上题可知,OA=OB=AB=![]() ,∴△AOB是正三角形,∴∠AOB=60°,∠AOC=120°,∴S△AOB=
,∴△AOB是正三角形,∴∠AOB=60°,∠AOC=120°,∴S△AOB=![]() ,S△AOC=
,S△AOC=![]() ,∴S=2(S扇形OAC﹣S△AOC)+S扇形OAB﹣S△AOB=2(
,∴S=2(S扇形OAC﹣S△AOC)+S扇形OAB﹣S△AOB=2(![]() ﹣
﹣![]() )+(
)+(![]() ﹣
﹣![]() )=
)=![]() π﹣
π﹣![]() ,∴打掉墙体面积为(
,∴打掉墙体面积为(![]() π﹣
π﹣![]() )平方米.
)平方米.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目