题目内容
【题目】在△ABC中,D是AB上一点,且AC2=ABAD,BC2=BABD,求证:CD⊥AB.
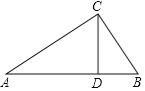
【答案】见解析。
【解析】
根据AC2=ADAB,BC2=BDAB,得出△ACD∽△ABC,△BDC∽△BCA,根据相似三角形的性质得出∠ADC=∠ACB、∠BDC=∠BCA,根据∠ADC+∠BDC=180°,∠ADC=∠BDC=90°解答.
解:证明:∵AC2=ADAB,
∴![]() =
=![]() ,又∠A=∠A,
,又∠A=∠A,
∴△ACD∽△ABC,
∴∠ADC=∠ACB.
∵BC2=BDAB,
∴![]() =
=![]() ,又∠B=∠B,
,又∠B=∠B,
∴△BDC∽△BCA,
∴∠BDC=∠BCA.
∴∠ADC=∠BDC.
∵点D为边AB上一点,
∴∠ADC+∠BDC=180°,
∴∠ADC=∠BDC=90°,
∴CD⊥AB.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目