��Ŀ����
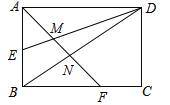
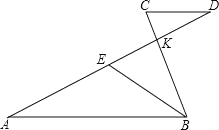
����Ŀ����ͼ����֪�߶�AB��CD��AD��BC�ཻ�ڵ�K��E���߶�AD��һ���㣬
(1)��BK��![]() KC����
KC����![]() ��ֵ��
��ֵ��
(2)����BE����BEƽ�֡�ABC����AE��![]() ADʱ�������߶�AB��BC��CD����֮����������������ϵ����д����Ľ��۲�����֤����
ADʱ�������߶�AB��BC��CD����֮����������������ϵ����д����Ľ��۲�����֤����
(3)��̽������BEƽ�֡�ABC����AE��![]() AD(n��2)ʱ���߶�AB��BC��CD����֮����������������ϵ����ֱ��д����Ľ��ۣ�����֤����
AD(n��2)ʱ���߶�AB��BC��CD����֮����������������ϵ����ֱ��д����Ľ��ۣ�����֤����
���𰸡�(1)![]() ��(2)AB��BC+CD��(3)AB��
��(2)AB��BC+CD��(3)AB��![]() BC+
BC+![]() CD��
CD��
��������
��1�����ݱ��������ʵõ�![]() ���������������ε����ʼ��㼴�ɣ�
���������������ε����ʼ��㼴�ɣ�
��2������BD��ȡBD���е�F������EF��BC��G�����������ε���λ�߶����õ�GF=![]() CD��EF=
CD��EF=![]() AB������ƽ���ߵ����ʡ���ƽ���ߵĶ���õ�EG=
AB������ƽ���ߵ����ʡ���ƽ���ߵĶ���õ�EG=![]() BC�����ɵõ��𰸣�
BC�����ɵõ��𰸣�
��3������BD����EF��AB��BC��G����BD��F�����ݱ��������ʡ����գ�2����������ɣ�
�⣺(1)��BK��![]() KC��
KC��
��![]() ��
��![]() ��
��
��AB��CD��
���CKD�ס�BKA��
��![]() ��
��![]() ��
��![]() ��
��
(2)���룺AB��BC+CD��
֤��������BD��ȡBD���е�F������EF��BC��G��
����λ�߶�������EF��AB��CD��
��GΪBC���е㣬��GEB����EBA��
�֡ߡ�EBA����GBE��
���GEB����GBE��
��EG��BG��![]() BC����GF��
BC����GF��![]() CD��EF��
CD��EF��![]() AB��
AB��
��EF��EG+GF��
����![]() AB��
AB��![]() BC+
BC+![]() CD��
CD��
��AB��BC+CD��
(3)���룺AB��![]() BC+
BC+![]() CD��
CD��
֤��������BD����EF��AB��BC��G����BD��F��
��AE��![]() AD��
AD��
��![]() ��
��![]() ��
��
��EF��AB��
��![]() ��
��![]() ��
��![]() ����EF��
����EF��![]() AB��
AB��
��EF��AB��AB��CD��
��EF��CD��
ͬ����BG��![]() BC��GF��
BC��GF��![]() CD��
CD��
��EF��EG+GF��
����![]() AB��
AB��![]() BC+
BC+![]() CD��
CD��
��AB��![]() BC+
BC+![]() CD��
CD��
�ʴ�Ϊ��(1)![]() ��(2)AB��BC+CD��(3)AB��
��(2)AB��BC+CD��(3)AB��![]() BC+
BC+![]() CD��
CD��

����Ŀ���������ǵIJɻ�ë����ǰ�裬�ɱ�ÿ��400Ԫ��ij�賡���괺����Ӫ����ÿ�ܵ�������y��������۵���x��Ԫ/���һ�κ��������������¹�ϵ��
x��Ԫ/� | 450 | 500 | 600 |
y��� | 350 | 300 | 200 |
��1������ݱ��е��������y��x֮��ĺ�����ϵʽ��
��2��������ÿ���Ҷ�������ܳ���40%���ò賡ÿ�ܻ���������30000Ԫ����ȷ�����۵���x��ȡֵ��Χ��