题目内容
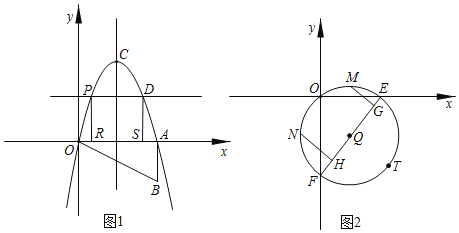
【题目】如图1，已知线段
、
相交于点O，连接
、
.
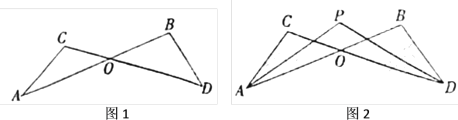
（1）求证：
；
（2）如图2，
与
的平分线
、
相交于点P，求证：
.
【答案】（1）证明见详解；（2）证明见详解.
【解析】
（1）根据三角形的内角和是180°和对顶角的性质即可得到结论；
（2）由（1）的证明方法可得∠P+∠CDP=∠C+∠CAP，∠P+∠BAP=∠B+∠BDP，根据AP、DP分别平分∠CAB和∠BDC，得到∠BAP=∠CAP，∠CDP=∠BDP，化简即可得到
.
（1）证明：在图1中，有∠A+∠C=180°-∠AOC，∠B+∠D=180°-∠BOD，
∵∠AOC=∠BOD，
∴∠A+∠C=∠B+∠D；
（2）由（1）的证明方法可得：
∠P+∠CDP=∠C+∠CAP，
∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP，
∵AP、DP分别平分∠CAB和∠BDC，
∴∠BAP=∠CAP，∠CDP=∠BDP，
∴化简可得：2∠P=∠B+∠C，
练习册系列答案
名校课堂系列答案
相关题目
