��Ŀ����
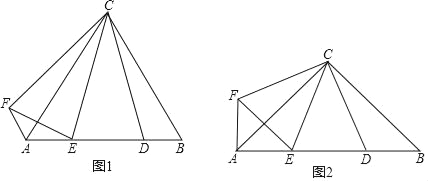
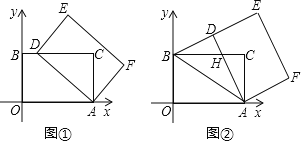
����Ŀ����ƽ��ֱ������ϵ�У��ı���AOBC�Ǿ��Σ���O��0��0������A��5��0������B��0��3�����Ե�AΪ���ģ�˳ʱ����ת����AOBC���õ�����ADEF����O��B��C�Ķ�Ӧ��ֱ�ΪD��E��F��
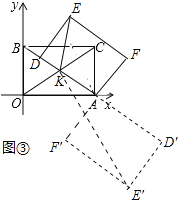
��1����ͼ�٣�����D����BC����ʱ�����D�����ꣻ
��2����ͼ�ڣ�����D�����߶�BE��ʱ��AD��BC���ڵ�H��
����֤��ADB�ա�AOB��
�����H�����꣮
��3����KΪ����AOBC�Խ��ߵĽ��㣬SΪ��KDE���������S��ȡֵ��Χ��ֱ��д��������ɣ���
���𰸡���1��D��1��3������2���������������H��![]() ��3������3��
��3������3��![]() ��S��
��S��![]() ��
��
��������
��1����ͼ�٣���Rt��ACD�����CD���ɽ�����⣻
��2���ٸ���HL֤�����ɣ�
�ڣ���AH=BH=m����HC=BC-BH=5-m����Rt��AHC�У�����AH2=HC2+AC2�������������m���ɽ�����⣻
��3����ͼ���У�����D���߶�BK��ʱ����DEK�������С������D��BA���ӳ�����ʱ����D��E��K������������������Сֵ�Լ����ֵ���ɽ�����⣻
��1����ͼ���У�
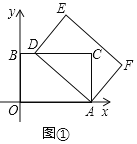
��A��5��0����B��0��3����
��OA=5��OB=3��
���ı���AOBC�Ǿ��Σ�
��AC=OB=3��OA=BC=5����OBC=��C=90�㣬
�߾���ADEF���ɾ���AOBC��ת�õ���
��AD=AO=5��
��Rt��ADC��CD=![]() =4��
=4��
��BD=BC-CD=1��
��D��1��3����
��2������ͼ���У�
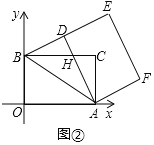
���ı���ADEF�Ǿ��Σ��õ���ADE=90�㣬
�ߵ�D���߶�BE�ϣ�
���ADB=90�㣬
�ɣ�1����֪��AD=AO����AB=AB����AOB=90�㣬
��Rt��ADB��Rt��AOB��HL����
����ͼ���У��ɡ�ADB�ա�AOB���õ���BAD=��BAO��
���ھ���AOBC�У�OA��BC��
���CBA=��OAB��
���BAD=��CBA��
��BH=AH����AH=BH=m����HC=BC-BH=5-m��
��Rt��AHC����AH2=HC2+AC2��
��m2=32+��5-m��2��
��m=![]() ��
��
��BH=![]() ��
��
��H��![]() ��3����
��3����
��3����ͼ���У�����D���߶�BK��ʱ����DEK�������С����Сֵ=![]() DEDK=
DEDK=![]() ��3����5-
��3����5-![]() ��=
��=![]() ��
��
����D��BA���ӳ�����ʱ����D��E��K��������������=![]() ��D��E���KD��=
��D��E���KD��=![]() ��3����5+
��3����5+![]() ��=
��=![]() ��
��
����������![]() ��S��
��S��![]() ��
��

 С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д� ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�����Ŀ��С��ͬѧ������ȫ��50��ͬѧ�ֱ�ϲ��������СƷ���������赸��Ŀ����������Ƴ������ͳ�Ʊ���
��ϲ���Ľ�Ŀ����� | ���� | ���� | �ٷֱȣ�%�� |
���� | �� | 9 | 12 |
СƷ | ������ | 21 | 42 |
���� | ���� | 10 | 28 |
�赸 | �� | 6 | 12 |
�ڱ��е������У�����һ���Ŀ��ͳ������ȫ��ȷ�ģ������ͳ������ǣ� ��
A. ����B. �赸C. ����D. СƷ