题目内容
【题目】如图，先对折矩形得折痕MN，再折纸使折线过点B，且使得A在MN上，这时折线EB与BC所成的角为（ ）
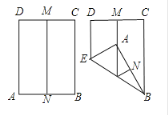
A.30°B.45°C.60°D.75°
【答案】C
【解析】
延长EA交BC于点F，根据折叠的性质可得DE∥MA∥CB，∠EAB=90°，DM=CM，2∠EBA＋∠FBA=90°，然后根据平行线分线段成比例定理证出EA=FA，然后根据垂直平分线的性质可得BE=BF，然后根据三线合一结合已知条件即可求出结论．
解：延长EA交BC于点F
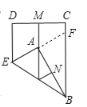
由折叠可得：DE∥MA∥CB，∠EAB=90°，DM=CM，2∠EBA＋∠FBA=90°
∴EA：FA=DM：CM=1，
∴EA=FA
∴AB垂直平分EF
∴BE=BF
∴∠EBA=∠FBA
∴3∠EBA=90°
∴∠EBA=30°
∴∠EBF=∠EBA＋∠FBA=60°
即折线EB与BC所成的角为60°
故选C．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
