题目内容
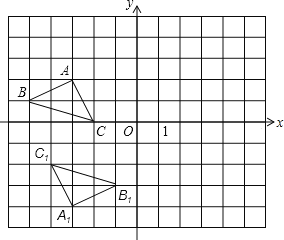
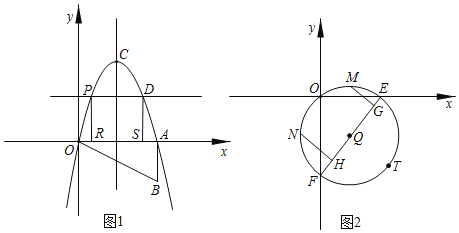
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆针旋转90°,点B旋转到点C的位置,一条抛物找正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点D,分别过点P,点D作x轴的垂线,交x轴于R,S两点,问:四边形PRSD的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
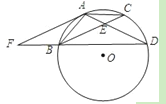
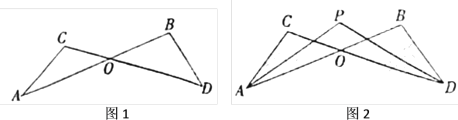
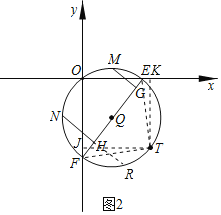
(3)如图2,把点B向下平移两个单位得到点T,过O,T两点作⊙Q交x轴,y轴于E,F两点,若M、N分别为弧![]() 、
、![]() 的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
【答案】(1)y=-x2+4x;(2)当a=1时,矩形PEFM的周长有最大值10;(3)MG+NH=4.
【解析】
(1)根据旋转变换的性质求出点C的坐标,利用待定系数法求出抛物线的解析式;
(2)设点P的坐标为P(a,-a2+4a),根据抛物线的对称性求出RS,根据二次函数的性质计算;
(3)作TK⊥x轴于K,TJ⊥y轴于J,连接TF,TE,延长NH交⊙Q于R,证明△ETK≌△FTJ,根据全等三角形的性质得到EK=FJ,得到OE+OF=8,根据垂径定理得到NH=NR=![]() OF,计算即可.
OF,计算即可.
解:(1)设y=ax2+bx+c,
∵OA=4,AB=2,
∴点A的坐标为(4,0),点B的坐标为(4,-2),
△AOB绕点O逆时针旋转90°,点B旋转到点C的位置,
∴点C的坐标为(2,4),
则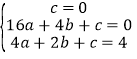
解得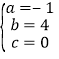 .
.
所以抛物线的解析式为y=-x2+4x;
(2)有最大值.
理由如下:设点P的坐标为P(a,-a2+4a),PR=DS=-a2+4a,
由抛物线的对称性知OR=AS,RS=PD=4-2a,
矩形PRSD的周长=2[4-2a+(-a2+4a)]=-2(a-1)2+10,
所以当a=1时,矩形PEFM的周长有最大值10;
(3)作TK⊥x轴于K,TJ⊥y轴于J,连接TF,TE,延长NH交⊙Q于R,
由题意得,点T的坐标为(4,-4,),即TJ=TK=4,
∴点T在∠EOF的平分线上,
∴![]() =
=![]()
∴TE=TF,
在Rt△TKE和Rt△TJF中,
![]() ,
,
∴△ETK≌△FTJ(HL),
∴EK=FJ,∠EOF=∠KTJ=90°,
∴OE+OF=OK-EK+OJ+FJ=OJ+OK=8,
∴EF为⊙Q的直径,
∴![]() =
=![]() ,
,
∵N为![]() 的中点,
的中点,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴NR=OF,
∴NH=NR=![]() OF,
OF,
同理MG=![]() OE,
OE,
∴MG+NH=![]() (OE+OF)=
(OE+OF)=![]() ×8=4.
×8=4.

 名校课堂系列答案
名校课堂系列答案