题目内容
【题目】求证:在直角三角形中至少有一个角不大于45°.
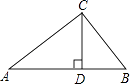
已知:如图所示,△ABC中,∠C=90°,求证:∠A,∠B中至少有一个不大于45°.
证明:假设__________,则∠A__________45°,∠B______45°. ∴∠A+∠B+∠C>45°+ _______+__________,这与________________________相矛盾. 所以___________不能成立,所以∠A,∠B中至少有一个角不大于45°.

【答案】∠A,∠B都大于45° > > 45° 90° 三角形内角和为180° 假设
【解析】
假设命题的结论不成立或假设命题的结论的反面成立,然后推出矛盾,说明假设错误,结论成立.
证明:假设∠A,∠B都大于45°,则∠A>45°,∠B>45°,
∴∠A+∠B+∠C>45°+ 45°+90°,这与三角形内角和为180°相矛盾,
所以假设不能成立,
所以∠A,∠B中至少有一个角不大于45°.

练习册系列答案
相关题目