题目内容
【题目】如图,△ABC中,CD⊥AB,垂足为D.下列条件中,能证明△ABC是直角三角形的有
①∠A+∠B=90°
②AB2=AC2+BC2
③ ![]()
④CD2=ADBD.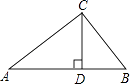
【答案】①②④
【解析】解:①∵三角形内角和是180°,由①知∠A+∠B=90°,
∴∠ACB=180°﹣(∠A+∠B)=180°﹣90°=90°,
∴△ABC是直角三角形.所以答案是:项①正确.②AB,AC,BC分别为△ABC三个边,由勾股定理的逆定理可知,②正确.③题目所给的比例线段不是△ACB和△CDB的对应边,且夹角不相等,无法证明△ACB与△CDB相似,也就不能得到∠ACB是直角,故③错误;④若△ABC是直角三角形,已知CD⊥AB,
又∵CD2=ADBD,(即 ![]() )
)
∴△ACD∽△CBD
∴∠ACD=∠B
∴∠ACB=∠ACD+∠DCB=∠B+∠DCB=90°
△ABC是直角三角形
∴所以答案是:项④正确;
所以答案是:①②④.
【考点精析】通过灵活运用勾股定理的逆定理和相似三角形的判定与性质,掌握如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目