题目内容
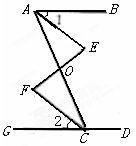
如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC.

理由如下:∵AD⊥BC于D,EG⊥BC于G,( 已知 )
∴∠ADC=∠EGC=90°,( )
∴AD∥EG,( )
∴∠1=∠2,( )
=∠3,( )
又∵∠E=∠1,( )
∴∠2=∠3 ( )
∴AD平分∠BAC.( )

理由如下:∵AD⊥BC于D,EG⊥BC于G,( 已知 )
∴∠ADC=∠EGC=90°,( )
∴AD∥EG,( )
∴∠1=∠2,( )
=∠3,( )
又∵∠E=∠1,( )
∴∠2=∠3 ( )
∴AD平分∠BAC.( )
垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;两直线平行,同位角相等;已知;等量代换;角平分线定义
试题分析:根据垂直的定义、平行线的判定和性质、角平分线的性质依次分析即可.
∵AD⊥BC于D,EG⊥BC于G,(已知)
∴∠ADC=∠EGC=90°,( 垂直的定义 )
∴AD∥EG,( 同位角相等,两直线平行 )
∴∠1=∠2,( 两直线平行,内错角相等 )
∠E=∠3,( 两直线平行,同位角相等 )
又∵∠E=∠1( 已知 )
∴∠2=∠3( 等量代换 )
∴AD平分∠BAC( 角平分线定义 ).
点评:平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
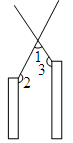

 ,
, ,则
,则 的度数是
的度数是