题目内容
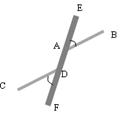
如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
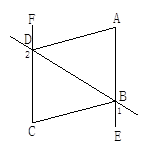
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
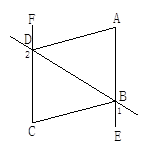
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
(1)可证明∠1=∠CDB,所以会平行。(2) 可证明∠A=∠CBE,所以AD和BC平行;(3)可证明∠FDA=∠A=∠CBE,∠ADB=∠CBD ,所以∠EBC=∠CBD。
试题分析:
(1)平行 :因为∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义) 所以∠1=∠CDB 所以AE∥FC( 同位角相等两直线平行)
(2)平行,因为AE∥CF,所以∠C=∠CBE(两直线平行, 内错角相等)又∠A=∠C 所以∠A=∠CBE
所以AF∥BC(两直线平行,内错角相等)
(3)平分:因为DA平分∠BDF,所以∠FDA=∠ADB 因为AE∥CF,AD∥BC 所以∠FDA=∠A=∠CBE,∠ADB=∠CBD ,所以∠EBC=∠CBD
点评:本题难度较低,主要考查学生对平行线判定与性质知识的掌握与应用。牢固掌握性质定理,注意数形结合思想培养,运用到考试中去。

练习册系列答案
相关题目

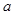 、
、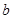 被
被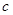 、
、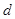 所截,且
所截,且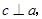
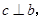
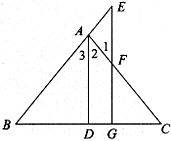
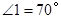 ,求∠3的大小.
,求∠3的大小. ,
,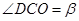 ,则
,则 的度数是__________。
的度数是__________。