题目内容
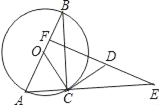
【题目】如图,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG,

(1)当∠ADE=15°时,求∠DGC的度数;
(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;
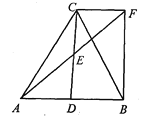
(3)如图2, 当点F落在对角线BD上时,点M为DE的中点,连接AM,FM,请你判断四边形AGFM的形状,并证明你的结论。
【答案】(1) ∠DGC=45°; (2) ∠DGC=45°不会变化; (3) 四边形AGFM是正方形
【解析】
(1)根据对称性及正方形性质可得∠CDF=60°=∠DFC,再利用三角形外角∠DFC=∠FDE+∠DPF可求∠DPC度数;
(2)由(1)知△DFC为等腰三角形,得出DF=DC,求出∠DFC=45+∠EDF,由∠DFC=∠DGC+∠EDF可得∠DGC=45;
(3)证明FG=MF=MA=AG,∠AGF=90,即可得出结论.
(1)△FDE与ADE关于DE对称
∴△FDE≌△ADE
∴∠FDE=∠ADE=15,AD=FD
∴∠ADF=2∠FDE=30
∵ABCD为正方形
∴AD=DC=FD,∠ADC=∠DAC=∠DFE=90
∴∠FDC=∠ADC-∠ADF=60
∴△DFC为等边三角形
∴∠DFC=60
∵∠DFC为△DGF外角
∴∠DFC=∠FDE+∠DGC
∴∠DGC=∠DFC-∠FDE=60-15=45
(2)不变.
证明: 由(1)知△DFC为等腰三角形,DF=DC
∴∠DFC=∠DCF=![]() (180-∠CDF) =90-
(180-∠CDF) =90-![]() ∠CDF①
∠CDF①
∵∠CDF=90-∠ADF=90-2∠EDF②
将②代入①得∠DFC=45+∠EDF
∵∠DFC=∠DGC+∠EDF
∴∠DGC=45
(3)四边形AMFG为正方形.
证明: ∵M为Rt△ADE中斜边DE的中点
∴AM=![]() DE
DE
∵M为Rt△FED中斜边DE的中点
∴FM=![]() DE=AM=MD
DE=AM=MD
由(1)知△AED≌△FED ∴AD=DF,∠ADG=∠FDG
△ADG与△FDG中,
AD=DF, ∠ADG=∠FDG,DG=DG
∴△ADG≌△FDG,
由(2)知∠DGC=45
∴∠DGA=∠DGF=45,AG=FG, ∠AGF=∠DGA+∠DGF=90
∵DB为正方形对角线,
∴∠ADB=∠45,
∵∠ADG=∠GDF=![]() ∠ADB=22.5
∠ADB=22.5
∵DM=FM
∴∠GDF=∠MFD=22.5
∵∠GMF=∠GDF+∠MFD=45
∴∠GMF=∠DGF=45
∴MF=FG
∴FG=MF=MA=AG,∠AGF=90
∴四边形AMFG为正方形。