题目内容
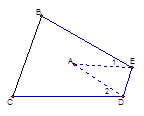
【题目】如图,平行四边形ABCD中,P是四边形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1 , S2 , S3 , S4 , 则一定成立的是( ) 
A.S1+S2>S3+S4
B.S1+S2=S3+S4
C.S1+S2<S3+S4
D.S1+S3=S2+S4
【答案】BD
【解析】解:∵四边形ABCD是平行四边形, ∴设S△ACD=S△ABC= ![]() SABCD=S,
SABCD=S,
∵S1= ![]() S△ABC=
S△ABC= ![]() S,S2=
S,S2= ![]() S△ABC=
S△ABC= ![]() S,S3=
S,S3= ![]() S△ACD=
S△ACD= ![]() S,S4=
S,S4= ![]() S△ACD=
S△ACD= ![]() S,
S,
∴S1+S3= ![]() S+
S+ ![]() S=S,S2+S4=
S=S,S2+S4= ![]() S+
S+ ![]() S=S,
S=S,
∴S1+S3=S2+S4 ,
S1+S2=S3+S4 .
故选B,D.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目