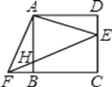
题目内容
【题目】已知,△ABC内接于圆O,弦CD⊥AB交AB于E,AF⊥BC于点F,AF交CD于点G.
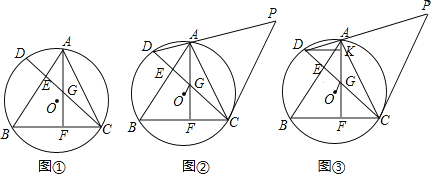
(1)如图①,求证:DE=EG;
(2)如图②,连接OG,连接DA并延长至点P,连接CP,点P在CG的垂直平分线上,若AP=2AG,求证:OG∥AB;
(3)如图③,在(2)的条件下,过点D作DK⊥AF于点K,若∠PAC=∠DAF,KG=![]() ,求线段CG的长.
,求线段CG的长.
【答案】(1)证明见解析;(2)证明见解析;(3)GC=2![]() .
.
【解析】
(1)连接AD,由余角的性质可得∠ABC=∠FGC,可得∠D=∠AGD,由等腰三角形的性质可得DE=EG;
(2)连接PG,过点P作PH⊥DC于点H,由线段垂直平分线的性质和等腰三角形的性质可得GH=HC,由平行四边形的性质可得![]() =
=![]() ,可得EH=2DE,可得GH=DE=EG=HC,由垂径定理可得OG⊥CD,即可证OG∥AB;
,可得EH=2DE,可得GH=DE=EG=HC,由垂径定理可得OG⊥CD,即可证OG∥AB;
(3)过点C作CN∥AD交AF的延长线于点N,连接PN交CD于点H,连接EN,通过证明△ADG≌△NCG,可得AD=AG=GN=CN,通过证明△DKG≌△CFG,可得KG=GF=![]() ,FC=DK,由勾股定理可求CN=
,FC=DK,由勾股定理可求CN=![]() =AD=AG=GN,即可求CG的长.
=AD=AG=GN,即可求CG的长.
证明:(1)连接AD
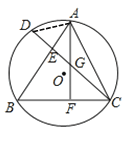
∵CD⊥AB,AF⊥BC
∴∠ABC+∠BCE=90°,∠BCE+∠FGC=90°
∴∠ABC=∠FGC,
∵∠D=∠ABC,∠FGC=∠AGD
∴∠D=∠AGD
∴AD=AG,且AE⊥CD
∴DE=EG,
(2)如图,连接PG,过点P作PH⊥DC于点H,
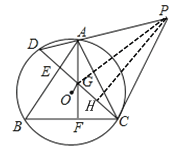
∵点P在CG的垂直平分线上,
∴PG=PC,且PH⊥DC
∴GH=HC
∵AB⊥CD,PH⊥CD
∴AB∥PH
∴![]()
∵AP=2AG,AD=AG
∴AP=2AD
∴![]() =
=![]()
∴EH=2DE
∵EH=EG+GH=2DE,且DE=EG
∴GH=DE=EG,且GH=HC
∴GH=DE=EG=HC
∴DG=GC,OG过圆心O
∴OG⊥CD,且AB⊥CD
∴OG∥AB
(3)如图,过点C作CN∥AD交AF的延长线于点N,连接PN交CD于点H,连接EN,
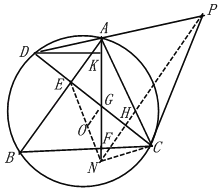
∵CN∥AD
∴∠DAN=∠ANC,∠ADC=∠DCN,且DG=CG
∴△ADG≌△NCG(AAS)
∴AD=NC,AG=AN,且AD=AG
∴AD=AG=GN=CN
∵AD∥CN
∴∠PAC=∠ACN,且∠DAN=∠ANC,∠PAC=∠DAN
∴∠ANC=∠ACN
∴AN=AC
∵∠DKG=∠GFC,∠DGK=∠CGF,DG=GC
∴△DKG≌△CFG(AAS)
∴KG=GF=![]() ,FC=DK
,FC=DK
∵FC2=CN2﹣NF2=AC2﹣AF2,
∴CN2﹣(CN﹣![]() )2=(2CN)2﹣(CN+
)2=(2CN)2﹣(CN+![]() )2,
)2,
∴CN=![]() =AD=AG=GN
=AD=AG=GN
∴NF=CN﹣![]() =
=![]()
∴FC=![]() =5,
=5,
∴GC=![]() =2
=2![]()