题目内容
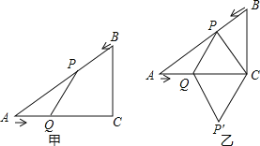
【题目】如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为ts(0<t<4)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值.
【答案】![]() .
.
【解析】
先判断出PE⊥AC,QE=EC,再判断出△APE≌△ABC,进而得出
![]() ,建立方程即可得出结论.
,建立方程即可得出结论.
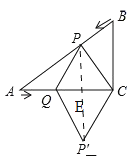
解:如图,连接PP',PP'交QC于E,当四边形PQP'C为菱形时,PE垂直平分QC,
即:PE⊥AC,QE=EC,
∵PE∥BC,
∴△APE∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
∵0<![]() <4,
<4,
∴当四边形PQP'C为菱形时,t的值为![]() 秒.
秒.![]()

练习册系列答案
相关题目