题目内容
【题目】如图,△ABC中,AB=3,AC=4,BC=5,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )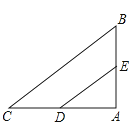
A.相切
B.相交
C.相离
D.无法确定
【答案】B
【解析】解答:过点A作AM⊥BC于点M,交DE于点N,
∴AM×BC=AC×AB,
∴AM=(3×4 )÷5= ![]()
∵D、E分别是AC、AB的中点,
∴DE∥BC,DE= ![]() BC=2.5,
BC=2.5,
∴AN=MN= ![]() AM,
AM,
∴MN=1.2,
∵以DE为直径的圆半径为1.25,
∴r=1.25>1.2,
∴以DE为直径的圆与BC的位置关系是:相交.
故选B.故选:B.
首先过点A作AM⊥BC,根据三角形面积求出AM的长,进而得出直线BC与DE的距离,进而得出直线与圆的位置关系.
【考点精析】本题主要考查了三角形的面积和三角形中位线定理的相关知识点,需要掌握三角形的面积=1/2×底×高;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目