题目内容
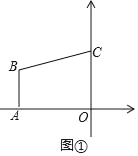
【题目】如图①,平面直角坐标系中,O为原点,点A坐标为(﹣4,0),AB∥y轴,点C在y轴上,一次函数y=![]() x+3的图象经过点B、C.
x+3的图象经过点B、C.

(1)点C的坐标为_____,点B的坐标为_____;
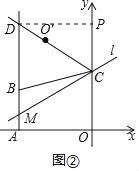
(2)如图②,直线l经过点C,且与直线AB交于点M,O'与O关于直线l对称,连接CO'并延长,交射线AB于点D.
①求证:△CMD是等腰三角形;
②当CD=5时,求直线l的函数表达式.
【答案】 (0,3) (﹣4,2) (2)见解析 (3) y=![]() x+3
x+3
【解析】试题分析:(1)设点C的坐标为(0,y),把x=0代入y=![]() x+3中得y=3,即可求出C点的坐标;设点B的坐标为(-4,y),把x=-4代入y=
x+3中得y=3,即可求出C点的坐标;设点B的坐标为(-4,y),把x=-4代入y=![]() x+3中得y=2,即可求出B点的坐标;
x+3中得y=2,即可求出B点的坐标;
(2)①根据对称的性质和平行线的性质,推知∠CMD=∠MCD,故MD=CD,所以CMD是等腰三角形;
②如图②,过点D作DP⊥y轴于点P.利用勾股定理求得CP的长度,然后结合坐标与图形的性质求得点M的坐标,利用待定系数法求得直线l的解析式即可.
试题解析:
(1)如图①,∵A(﹣4,0),AB∥y轴,直线y=![]() x+3经过点B、C,
x+3经过点B、C,
设点C的坐标为(0,y),把x=0代入y=vx+3x+3中得y=3,
∴C(0,3);
设点B的坐标为(﹣4,y),把x=4代入y=![]() x+3中得y=2,
x+3中得y=2,
∴B(﹣4,2);
故答案是:(0,3);(﹣4,2);
(2)①证明:∵AB∥y轴,
∴∠OCM=∠CMD.
∵∠OCM=∠MCD,
∴∠CMD=∠MCD,
∴MD=CD,
∴CMD是等腰三角形;
②如图②,过点D作DP⊥y轴于点P.
在直角△DCP中,由勾股定理得到:CP=![]() =3,
=3,
∴OP=AD=CO+CP=3+3=6,
∴AB=AD﹣DM=6﹣5=1,
∴点M的坐标是(﹣4,1).
设直线l的解析式为y=kx+b(k≠0).
把M(﹣4,1)、C(0,3)分别代入,得
![]() ,
,
解得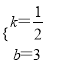
故直线l的解析式为y=![]() x+3.
x+3.