题目内容
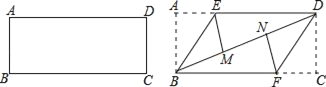
【题目】准备一张矩形纸片,按如图操作:
将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,BE=2,求菱形BFDE的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据矩形的性质和翻折变换的性质得到∠EBD=∠FDB,证明EB∥DF,根据平行四边形的判定定理证明结论;
(2)根据菱形的性质和翻折变换的性质求出∠ABE=30°,根据直角三角形的性质求出AB=![]() ,根据菱形的面积公式计算即可.
,根据菱形的面积公式计算即可.
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD,AB∥CD,
∴∠ABD=∠CDB,
由翻折变换的性质可知,∠ABE=∠EBD,∠CDF=∠FDB,
∴∠EBD=∠FDB,
∴EB∥DF,
∵ED∥BF,
∴四边形BFDE为平行四边形;
(2)解:∵四边形BFDE为菱形,
∴∠EBD=∠FBD,
∵∠EBD=∠ABE,
∴∠EBD=∠FBD=∠ABE,
∵四边形ABCD是矩形,
∠ABC=90°,
∴∠EBD=∠FBD=∠ABE=30°,
∴AB=![]() ,
,
∴菱形BFDE的面积S=DE×AB=2![]() .
.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
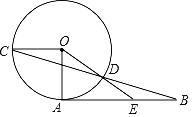
三点一测快乐周计划系列答案【题目】如图,AB是⊙O的直径,弦CD与AB相交,连接CO,过点D作⊙O的切线,与AB的延长线交于点E,若DE∥AC,∠BAC=40°,则∠OCD的度数为( )
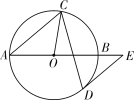
A.65°B.30°C.25°D.20°
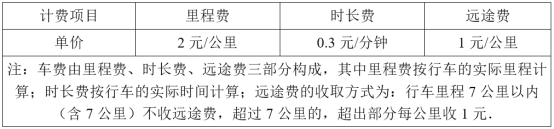
【题目】某便利店的咖啡单价为10元/杯,为了吸引顾客,该店共推出了三种会员卡,如下表:
会员卡类型 | 办卡费用/元 | 有效期 | 优惠方式 |
A类 | 40 | 1年 | 每杯打九折 |
B类 | 80 | 1年 | 每杯打八折 |
C类 | 130 | 1年 | 一次性购买2杯,第二杯半价 |
例如,购买A类会员卡,1年内购买50次咖啡,每次购买2杯,则消费![]() 元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为( )
元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为( )
A.购买A类会员卡B.购买B类会员卡
C.购买C类会员卡D.不购买会员卡
【题目】张老师将自己2019年10月至2020年5月的通话时长(单位:分钟)的有关数据整理如下:
①2019年10月至2020年3月通话时长统计表
时间 | 10月 | 11月 | 12月 | 1月 | 2月 | 3月 |
时长(单位:分钟) | 520 | 530 | 550 | 610 | 650 | 660 |
②2020年4月与2020年5月,这两个月通话时长的总和为1100分钟根据以上信息,推断张老师这八个月的通话时长的中位数可能的最大值为( )
A.550B.580C.610D.630