Question

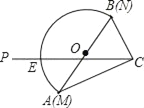
【题目】如图，已知：的直径与弦的夹角，过点作的切线交的延长线于点．

求证：；

的直径是，以点为圆心作圆，当半径为多长时，与相切？

若，求图中阴影部分的面积（结果精确到，）

Answer 1

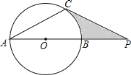
【答案】（1）见解析；（2）3；（3）4.1.

【解析】

（1）连接OC．根据圆周角定理即可求得∠COP=2∠ACO=60°，根据切线的性质定理以及直角三角形的两个锐角互余，求得∠P=30°，即可证明；

（2）如图连接BC．由圆周角定理知AC⊥BC，然后根据“AC与⊙B相切”知BC即为⊙B的半径．

（3）阴影部分的面积即为直角三角形OCP的面积减去扇形OCB的面积．

（1）如图，连接OC．

∵AO=OC，∴∠ACO=∠A=30°，∴∠COP=2∠ACO=60°．

∵PC切⊙O于点C，∴OC⊥PC．即∠OCP=90°，∴∠P=30°，∴∠A=∠P，∴AC=PC．

（2）如图，连接BC．

∵AB是⊙O的直径，∴∠ACB=90°，即AC⊥BC．

又∵AC与⊙B相切，∴BC即为⊙B的半径．

在直角△ACB中，∠A=30°，AB=6，则BC=AB=3；

（3）在Rt△OCP中，∵∠P=30°，∴tan∠P==，∴OC=2．

∵S△OCP=CPOC=×6×2=6，S扇形COB=2π，∴S阴影=S△OCP﹣S扇形COB=6﹣2π≈4.1．