题目内容
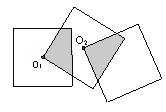
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠AOM= 度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 .
【答案】(1)120;(2)∠AOM﹣∠NOC=30°,理由参见解析;(3)6或24秒.
【解析】
试题分析:(1)由角平分线意义可得∠BOM=120°÷2=60°,根据平角的意义可算出∠AOM的度数;(2)如图3,∠AOM转化成∠MON-∠AON,∠NOC转化成∠AOC-∠AON,则∠AOM﹣∠NOC=(∠MON-∠AON)-(∠AOC-∠AON),即等于∠MON-∠AON-∠AOC+∠AON=∠MON-∠AOC=90-60=30度,从而推出∠AOM与∠NOC之间的数量关系;(3)若直线ON恰好平分∠AOC,当逆时针旋转60°时,ON平分∠AOC,或当逆时针旋转240°时,ON平分∠AOC,分别除以10,即为所求的旋转时间.
试题解析:(1)由题意可知:OM恰好平分∠BOC,∴∠BOM=120°÷2=60°,∴∠AOM=180°﹣60°=120°; (2)如图3,∵∠BOC=120°,∴∠A0C=60°,∠AOM转化成∠MON-∠AON,∠NOC转化成∠AOC-∠AON,∵∠AON=90°﹣∠AOM=60°﹣∠NOC,∴∠AOM﹣∠NOC=30°;(3)设三角板绕点O旋转的时间是x秒,∵∠BOC=120°,∴∠AOC=60°,当逆时针旋转60°或逆时针旋转240°时 ON平分∠AOC, 于是可列10x=60或10x=240,∴x=6或x=24,即此时三角板绕点O旋转的时间是6秒或24秒.故答案为:6秒或24秒.

 阅读快车系列答案
阅读快车系列答案【题目】今年冬天受寒潮影响,淘宝上的电热取暖器销售火爆.某电商销售每台成本价分别为200元、170元的A、B两种型号的电热取暖器,下表是近两天的销售情况:
销售时段 | |||
销售数量 | |||
A种型号 | B种型号 | 销售收入 | |
第一天 | 3台 | 5台 | 1800元 |
第二天 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电热取暖器的销售单价;
(2)若该电商准备用不多于5400元的金额再采购这两种型号的电热取暖器共30台,问A种型号的电热取暖器最多能采购多少台?