题目内容
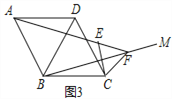
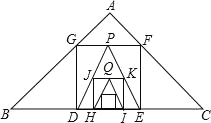
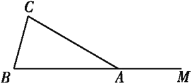
【题目】如图,在△ABC中,AB=AC,点M在BA的延长线上.
(1)按下列要求作图,并在图中标明相应的字母.(保留作图痕迹)
①作∠MAC的平分线AN;
②作AC的中点O,连结BO,并延长BO交AN于点D,连结CD;
(2)在(1)的条件下,判断四边形ABCD的形状,并证明你的结论.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)作一个角的平分线和线段的垂直平分线可完成作图;
(2)由AB=AC得∠ACB=∠ABC,由AN平分∠MAC得到∠MAN=∠CAN,则利用三角形外角的性质可得到∠ACB=∠CAD,所以BC∥AD,于是可证明△BOC≌△DOA,得到BC=AD,然后根据平行四边形的判定方法可判断四边形ABCD是平形四边形.
(1)作∠MAC的角平分线AN,作AC的中垂线得到AC的中点O,连接BO,并延长BO交AN于点D,连接CD,如图;
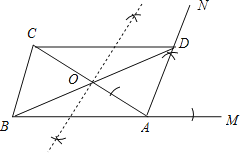
(2)四边形ABCD是平形四边形,理由如下:
∵AB=AC
∴∠ACB=∠ABC,
∵AN平分∠MAC,
∴∠MAN=∠CAN,
∵∠MAC=∠ABC+∠ACB,
∴∠ACB=∠CAD,
∴BC∥AD,
∵AC的中点是O
∴AO=CO,
在△BOC和△DOA中
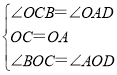
∴△BOC≌△DOA,
∴BC=AD,
而BC∥AD,
∴四边形ABCD是平形四边形.

【题目】某校在争创“全国文明城市”活动中,组织全体学生参加了“创文”知识竞赛,为了解各年级成绩情况,学校这样做的:
(收集数据)从七、八、九三个年级的竞赛成绩中各随机抽取了10名学生成绩如下表:
七年级 | 60 | 70 | 60 | 100 | 80 | 70 | 80 | 60 | 40 | 90 |
八年级 | 80 | 80 | 100 | 40 | 70 | 60 | 80 | 90 | 50 | 80 |
九年级 | 70 | 50 | 60 | 90 | 100 | 80 | 80 | 90 | 70 | 70 |
(整理、描述数据)(说明:80≤x≤100为优秀,60≤x<80为合格,40≤x<60为一般)
年级 | 40≤x<60 | 60≤x<80 | 80≤x≤100 |
七年级 | 1 | 5 | 4 |
八年级 | 2 | 2 | 6 |
九年级 | 1 | 4 | 5 |
年级 | 平均数 | 众数 | 中位数 |
七年级 | a | 60 | 70 |
八年级 | 73 | b | 80 |
九年级 | 76 | 70 | c |
(分析数据)三组样本数据的平均分、众数、中位数如上表所示,其中a= ,b= ,c= .
(得出结论)请你根据以上信息,推断你认为成绩好的年级,并说明理由(至少从两个角度说明)