��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���֪���κ�����ͼ��ԭ�㼰��A��1,2��
��x���ཻ����һ��B(3,0)������B����ƽ��3����λ�õ�C��
(1)������κ����Ľ���ʽ��
(2)����M���߶�OC�ϣ�ƽ������һ��Q��ʹ���ı���ABMQΪ���Σ����M���ꣻ
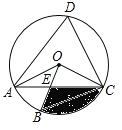
(3)����P���߶�OC�ϣ���O�������C���˶�����P����x��Ĵ��ߣ���ֱ��AO��D�㣬��PDΪ����PD���Ҳ���������PDEF����P���˶�ʱ����D����E����FҲ��֮�˶�����
������E�ڶ��κ�����ͼ����ʱ����OP�ij���
������P��O�������C���������˶����ٶ�Ϊÿ��1����λ���ȣ���P���˶�t��ʱ��ֱ��AC����DEΪֱ������M���У�ֱ��д���˿�t��ֵ��
���𰸡�(1)��y=-![]() +3x��(2)��M����Ϊ��1��0����3-2
+3x��(2)��M������1��0����3-2![]() ��0����3+2
��0����3+2![]() ��0����(3)������
��0����(3)������![]() ������t=
������t=![]() ��t=
��t=![]() .
.
��������
���������(1)��������κ����Ľ���ʽΪy=a![]() +bx+c�����ö��κ�����ͼ��ԭ�㼰��A��1��2����B��3��0�����ֱ�������a��b��c��ֵ���ɣ�(2)����M��AB�Ĵ�ֱƽ������x��Ľ��㣻M��B����߲���BM=AB��M��B���ұ߲���BM=AB������������ۿɵõ�M���ꣻ(3)������A����AH��x����H�㣬����DP��AH���ó���OPD�ס�OHA���������OP�ij�����������������ۣ����t��ֵ���ɣ�
+bx+c�����ö��κ�����ͼ��ԭ�㼰��A��1��2����B��3��0�����ֱ�������a��b��c��ֵ���ɣ�(2)����M��AB�Ĵ�ֱƽ������x��Ľ��㣻M��B����߲���BM=AB��M��B���ұ߲���BM=AB������������ۿɵõ�M���ꣻ(3)������A����AH��x����H�㣬����DP��AH���ó���OPD�ס�OHA���������OP�ij�����������������ۣ����t��ֵ���ɣ�
���������(1)������κ����Ľ���ʽΪy=a![]() +bx+c��
+bx+c��
�����κ�����ͼ��ԭ�㼰��A��1��2����B��3��0����
��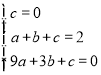 �����
�����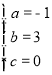 �� �ʶ��κ�������ʽΪ��y=-
�� �ʶ��κ�������ʽΪ��y=-![]() +3x��
+3x��
(2)��M��AB�Ĵ�ֱƽ������x��Ľ��㣬��M�����ǣ�1��0����
M��B����߲���BM=AB����M�����ǣ�3-2![]() ��0����
��0����
M��B���ұ߲���BM=AB����M�����ǣ�3+2![]() ��0����
��0����
�ʵ�M����Ϊ��1��0����3-2![]() ��0����3+2
��0����3+2![]() ��0����
��0����
(3)��������֪�ɵ�C��6��0����ͼ����A����AH��x����H�㣬
��DP��AH�����OPD�ס�OHA����![]() ����
����![]() ����PD=2a��
����PD=2a��
��������PDEF����E��3a��2a������E��3a��2a���ڶ��κ���y1=-x2+3x��ͼ���ϣ�
��a=![]() ����OP=
����OP=![]() ��
��
��ֱ��AC����DEΪֱ������M���У��˿�t��ֵΪ��t=![]() ��t=
��t=![]() .
.