题目内容
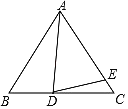
【题目】将一副直角三角板如图放置,使GM与AB在同一直线上,其中点M在AB的中点处,MN与AC交于点E,∠BAC=30°,若AC=9cm,则EM的长为( )
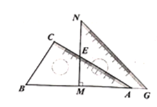
A. 2.5cm B. 3cm C. 4cm D. 4.5cm
【答案】B
【解析】
连接CM,因为点M在AB的中点处,所以由直角三角形斜边上的中线等于斜边的一半可得:CM=AM,△ACM是等腰三角形,再过点M作MF⊥AC于点F,因为∠MEF=60°,可得∠EMF=30°,利用三线合一得出CF=FA=![]() AC=4.5cm,设EM=x,则EF=
AC=4.5cm,设EM=x,则EF=![]() x,EA=EF+FA=
x,EA=EF+FA=![]() x+4.5,
x+4.5,
在Rt△AEM中,因为∠MAE=30°,所以ME=![]() AE,即x=
AE,即x=![]() (
(![]() x+4.5),解得x=3.
x+4.5),解得x=3.
解:连接CM,过点M作MF⊥AC于点F,
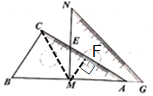
∵点M在AB的中点处,
∴CM=AM=AB,
∵MF⊥AC
∴CF=AF=![]() AC=4.5,
AC=4.5,
∵∠EAM=30°,
∴∠MEA=60° ∠EMF=30°,
设EM=x,则EF=![]() EM=
EM=![]() x,AE=AF+EF=4.5+
x,AE=AF+EF=4.5+![]() x
x
Rt△AME中,∵∠EAM=30°,
∴EM=![]() AE,即x=
AE,即x=![]() (4.5+
(4.5+![]() x),解得x=3,即EM=3.
x),解得x=3,即EM=3.
故答案为:3cm,

练习册系列答案
相关题目