题目内容
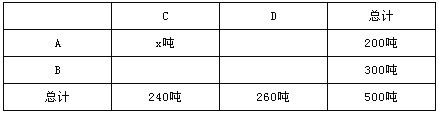
【题目】某乡A,B两村盛产香梨,A村有香梨200吨,B村有香梨300吨,现将这些香梨运到C,D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元.设从A村运往C仓库的香梨为x吨,A,B两村运香梨往两仓库的运输费用分别为yA元,yB元.
(1)请填写下表,并求出yA,yB与x之间的函数关系式;
(2)当x为何值时,A村的运费较少?
(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.
【答案】(1)填写如下:
C | D | 总计 | |
A | (200﹣x)吨 | ||
B | (240﹣x)吨 | (60+x)吨 |
yA=﹣5x+9000;yB=7x+7920;(2)x=200;(3)从A村运往C仓库0吨,运往D仓库为200吨,B村应往C仓库运240吨,运往D仓库60吨.
【解析】
试题(1)仔细阅读题意,根据A村有香梨200吨,B村有香梨300吨,C仓库可储存240吨,D仓库可储存260吨,从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元,即可得到结果;
(2)根据一次函数的性质即可求得结果;
(3)先表示出两村的运费之和,再根据一次函数的性质即可求得结果.
(1)填写如下:
C | D | 总计 | |
A | (200﹣x)吨 | ||
B | (240﹣x)吨 | (60+x)吨 |
由题意得:yA=40x+45(200﹣x)=﹣5x+9000;yB=25(240﹣x)+32(60+x)=7x+7920;
(2)对于yA=﹣5x+9000(0≤x≤200),
∵k=﹣5<0,
∴此一次函数为减函数,
则当x=200吨时,yA最小,其最小值为﹣5×200+9000=8000(元)
(3)设两村的运费之和为W,
则W=yA+yB=﹣5x+9000+7x+7920=2x+16920(0≤x≤200),
∵k=2>0,
∴此一次函数为增函数,
则当x=0时,W有最小值,W最小值为16920元.
此时调运方案为:从A村运往C仓库0吨,运往D仓库为200吨,B村应往C仓库运240吨,运往D仓库60吨.