题目内容
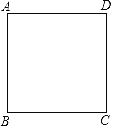
【题目】如图，电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动，电子蚂蚁P从点A出发，以
个单位长度/秒的速度绕正方形作顺时针运动，电子蚂蚁Q从点A出发，以
个单位长度秒的速度绕正方形作逆时针运动，则它们第2019次相遇在( )
A. 点AB. 点BC. 点CD. 点D
【答案】D
【解析】
设两只电子蚂蚁每隔x秒相遇一次，根据正方形周长=二者速度之和×时间，可得出关于x的一元一次方程，解之即可得出两只电子蚂蚁每隔2秒相遇一次，再结合电子蚂蚁Q的速度、出发点及运动方向可得出它们第1次、第2次、第3次、第4次、第5次……相遇点，结合2019÷4=504……3可得出结论．
解：设两只电子蚂蚁每隔x秒相遇一次，
根据题意得：（
+
）x=1×4，
解得：x=2．
∵电子蚂蚁Q从点A出发，以个单位长度/秒的速度绕正方形作逆时针运动，
∴它们第1次相遇在B点，第2次相遇在C点，第3次相遇在D点，第4次相遇在A点，第5次相遇在B点，第6次相遇在C点，…．
又∵2019÷4=504……3，
∴第2019次相遇和第3次相遇地点相同，即第2019次相遇在点D．
故选：D．
练习册系列答案
阅读快车系列答案
相关题目
