题目内容
【题目】如图,平行四边形ABCD中,∠BAD的平分线交BC边于点M,而MD平分∠AMC,若∠MDC=45°,则∠BAD= , ∠ABC=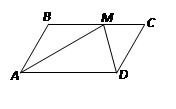
【答案】60°;120°
【解析】解:平行四边形ABCD,
∴BC∥AD,∠C=∠BAD,
∴∠AMC+∠MAD=180°,∠B+∠BAD=180°
∵∠BAD的平分线AM,MD平分∠AMC,
∴∠C=∠BAD=2∠MAD,∠AMD=∠CMD,
∵∠C+∠CMD+∠CDM=180°,∠MDC=45°,
即:∠MAD+2∠CMD=180°,且∠CMD+2∠MAD=135°,
解得:∠MAD=30°,
∴∠BAD=60°,∠ABC=120°.
故答案为:60°,120°
根据平行四边形的性质及平行线的性质证得∠C=∠BAD,∠AMC+∠MAD=180°,∠B+∠BAD=180°,再根据角平分线的定义证出∠C=∠BAD=2∠MAD,∠AMD=∠CMD,然后根据∠MDC=45°,得出∠CMD+2∠MAD=135°,及∠MAD+2∠CMD=180°,即可求出∠BAD、∠ABC的度数。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目