题目内容
【题目】如图,菱形ABCD中,AB=AC=2,点E、F是AB,AD边上的动点,且AE=DF,则EF长的最小值为 . 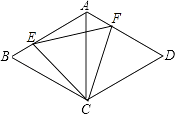
【答案】![]()
【解析】解:如图, 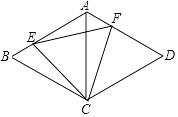
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=AC,
∴△ABC,△ACD都是等边三角形,
∴∠EAC=∠D=60°,
在△EAC和△FDC中,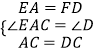 ,
,
∴△EAC≌△FDC,
∴EC=CF,∠ACE=∠DCF,
∴∠ECF=∠ACD=60°,
∴△ECF是等边三角形,
∴CE=EF=CF,
∵CE⊥AB时,线段CE最小,最小值为 ![]() ×2=
×2= ![]() ,
,
∴EF的最小值为 ![]() .
.
所以答案是 ![]() .
.
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目