题目内容
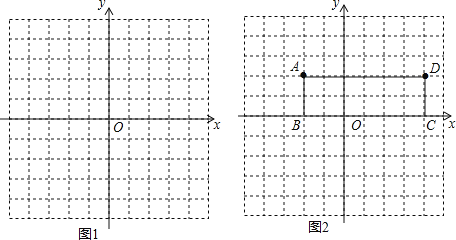
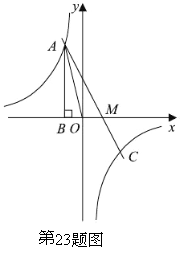
【题目】（2011贵州安顺，23，10分）如图，已知反比例函数
的图像经过第二象限内的点A（－1，m），AB⊥x轴于点B，△AOB的面积为2．若直线y=ax+b经过点A，并且经过反比例函数的图象上另一点C（n，一2）．
⑴求直线y=ax+b的解析式；
⑵设直线y=ax+b与x轴交于点M，求AM的长．
【答案】（1）∵点A（-1，m）在第二象限内，∴AB = m，OB = 1，∴
即：
，解得
，∴A (-1,4)，
∵点A (-1,4)，在反比例函数
的图像上，∴4 =
，解得
，
∵反比例函数为
，又∵反比例函数的图像经过C（n，
）
∴
，解得
，∴C (2,-2)，
∵直线
过点A (-1,4)，C (2,-2)
∴
解方程组得 
∴直线的解析式为
；
（2）当y = 0时，即
解得
，即点M（1，0）
在
中，∵AB = 4，BM = BO +OM = 1+1 = 2，
由勾股定理得AM=
．
【解析】略
练习册系列答案
名校课堂系列答案
相关题目
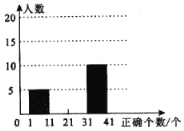
【题目】学校为了从李飞与刘亮中选取一人参加市射击比赛，现将他们某次射击训练的成绩绘制了如下图所示的折线统计图：
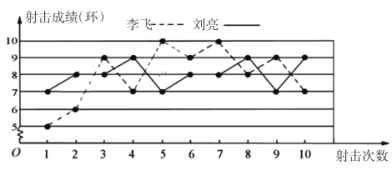
（1）请根据折线统计图中提供的信息填写下表：
平均数 | 中位 | 众数 | |
李飞 | 8 | ||
刘亮 | 8 | 8 |
（2）请计算李飞与刘亮射击训练的成绩的方差．（方差公式：
）
（3）从折线统计图上分析李飞与刘亮的射击成绩走势和稳定性，派谁去参加射击比赛更合适．
