ЬтФПФкШн
ЁОЬтФПЁПвбжЊжБЯпy=kx+3ЃЈ1-kЃЉЃЈЦфжаkЮЊГЃЪ§ЃЌkЁй0ЃЉЃЌkШЁВЛЭЌЪ§жЕЪБЃЌПЩЕУВЛЭЌжБЯпЃЌЧыЬНОПетаЉжБЯпЕФЙВЭЌЬиеїЃЎ
ЪЕМљВйзї
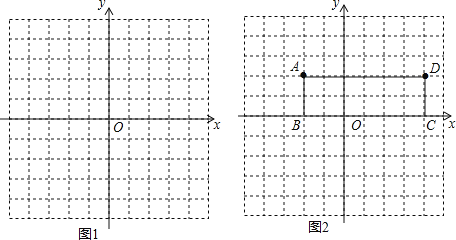
ЃЈ1ЃЉЕБk=1ЪБЃЌжБЯпl1ЕФНтЮіЪНЮЊ ЃЌЧыдкЭМ1жаЛГіЭМЯѓЃЛЕБk=2ЪБЃЌжБЯпl2ЕФНтЮіЪНЮЊ ЃЌЧыдкЭМ2жаЛГіЭМЯѓЃЛ
ЬНЫїЗЂЯж
ЃЈ2ЃЉжБЯпy=kx+3ЃЈ1-kЃЉБиОЙ§ЕуЃЈ ЃЌ ЃЉЃЛ
РрБШЧЈвЦ
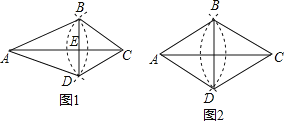
ЃЈ3ЃЉОиаЮABCDШчЭМ2ЫљЪОЃЌШєжБЯпy=kx+k-2ЃЈkЁй0ЃЉЗжОиаЮABCDЕФУцЛ§ЮЊЯрЕШЕФСНВПЗжЃЌЧыдкЭМжажБНгЛГіетЬѕжБЯпЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=xЃЌМћНтЮіЃЛy=2x-3ЃЌМћНтЮіЃЛЃЈ2ЃЉЃЈ3ЃЌ3ЃЉЃЛЃЈ3ЃЉМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉАбЕБk=1ЃЌk=2ЪБЃЌЗжБ№ДњШыЧѓвЛДЮКЏЪ§ЕФНтЮіЪНМДПЩЃЌ
ЃЈ2ЃЉРћгУkЃЈx-3ЃЉ=y-3ЃЌПЩЕУЮоТлkШЁКЮжЕЃЈ0Г§ЭтЃЉЃЌжБЯпy=kx+3ЃЈ1-kЃЉБиОЙ§ЕуЃЈ3ЃЌ3ЃЉЃЛ
ЃЈ3ЃЉЯШЧѓГіжБЯпy=kx+k-2ЃЈkЁй0ЃЉЮоТлkШЁКЮжЕЃЌзмЙ§ЕуЃЈ-1ЃЌ-2ЃЉЃЌдйШЗЖЈОиаЮЖдНЧЯпЕФНЛЕуМДПЩЛГіжБЯпЃЎ
ЃЈ1ЃЉЕБk=1ЪБЃЌжБЯпl1ЕФНтЮіЪНЮЊЃКy=xЃЌ
ЕБk=2ЪБЃЌжБЯпl2ЕФНтЮіЪНЮЊy=2x-3ЃЌ
ШчЭМ1ЃЌ
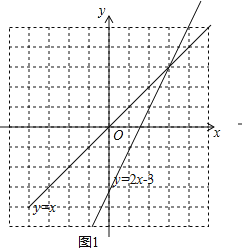
ЃЈ2ЃЉЁпy=kx+3ЃЈ1-kЃЉЃЌ
ЁрkЃЈx-3ЃЉ=y-3ЃЌ
ЁрЮоТлkШЁКЮжЕЃЈ0Г§ЭтЃЉЃЌжБЯпy=kx+3ЃЈ1-kЃЉБиОЙ§ЕуЃЈ3ЃЌ3ЃЉЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌ
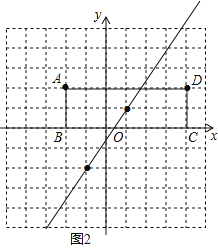
ЁпжБЯпy=kx+k-2ЃЈkЁй0ЃЉ
ЁрkЃЈx+1ЃЉ=y+2ЃЌ
ЁрЃЈkЁй0ЃЉЮоТлkШЁКЮжЕЃЌзмЙ§ЕуЃЈ-1ЃЌ-2ЃЉЃЌ
евГіЖдНЧЯпЕФНЛЕуЃЈ1ЃЌ1ЃЉЃЌЭЈЙ§СНЕуЕФжБЯпЦНЗжОиаЮABCDЕФУцЛ§ЃЎ

 ЦкФЉБІЕфЕЅдЊМьВтЗжРрИДЯАОэЯЕСаД№АИ
ЦкФЉБІЕфЕЅдЊМьВтЗжРрИДЯАОэЯЕСаД№АИЁОЬтФПЁПФГОЯњЩЬДгЪаГЁЕУжЊШчЯТаХЯЂЃК
ФГЦЗХЦПеЕїЩШ | ФГЦЗХЦЕчЗчЩШ | |
НјМлЃЈдЊ/ЬЈЃЉ | 700 | 100 |
ЪлМлЃЈдЊ/ЬЈЃЉ | 900 | 160 |
ЫћЯжга40000дЊзЪН№ПЩгУРДвЛДЮадЙКНјИУЦЗХЦПеЕїЩШКЭЕчЗчЩШЙВ100ЬЈЃЌЩшИУОЯњЩЬЙКНјПеЕїЩШ![]() ЬЈЃЌПеЕїЩШКЭЕчЗчЩШШЋВПЯњЪлЭъКѓЛёЕУРћШѓЮЊ
ЬЈЃЌПеЕїЩШКЭЕчЗчЩШШЋВПЯњЪлЭъКѓЛёЕУРћШѓЮЊ![]() дЊ.
дЊ.
ЃЈ1ЃЉЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЃЛ
ЕФКЏЪ§НтЮіЪНЃЛ
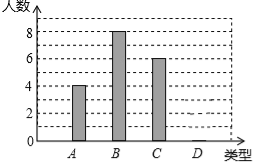
ЃЈ2ЃЉРћгУКЏЪ§аджЪЃЌЫЕУїИУОЯњЩЬШчКЮНјЛѕПЩЛёРћзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП