题目内容
如图，DE⊥AB，∠A=25°，∠D=45°，则∠ACB的度数为110°
110°
．分析：由DE与AB垂直，利用垂直的定义得到∠BED为直角，进而确定出三角形BDE为直角三角形，利用直角三角形的两锐角互余，求出∠B的度数，在三角形ABC中，利用三角形的内角和定理即可求出∠ACB的度数．
解答：解：∵DE⊥AB，
∴∠BED=90°，
∵∠D=45°，
∴∠B=45°，又∠A=25°，
∵∠ACB=180°-（∠A+∠B）=110°．
故答案为：110°
∴∠BED=90°，
∵∠D=45°，
∴∠B=45°，又∠A=25°，
∵∠ACB=180°-（∠A+∠B）=110°．
故答案为：110°
点评：此题考查了三角形的外角性质，直角三角形的性质，以及三角形的内角和定理，熟练掌握性质及定理是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
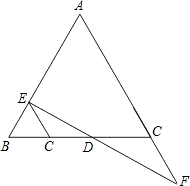（A类）如图，DE⊥AB、DF⊥AC．垂足分别为E、F．请你从下面三个条件中，再选出两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情况）．
如图，DE∥AB，AC=2，CE=4，△ABC的面积是5，求△DCE的面积．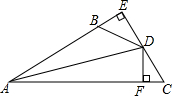
如图，DE⊥AB于E，DF⊥AC于F，若BD=CD，BE=CF
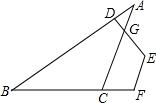如图，DE⊥AB，EF∥AC，∠A=32°，求∠DEF的度数．