题目内容
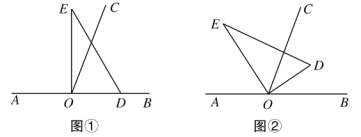
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角板的直角顶点放在点O处(∠DOE=90°).
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O转动,若OD恰好平分∠BOC,求∠AOE的度数。
【答案】(1)20;(2)55°
【解析】
(1)根据角的和差得出∠COE=∠DOE-∠BOC,代入求出即可;
(2)根据角平分线定义求出∠BOD =35°,再根据角的和差得出∠BOE=∠BOD+∠DOE=125°,再根据∠AOE=180°-∠BOE即可;
解:(1)如图①,∵∠BOC=70°,∠DOE=90°
∴∠COE=∠DOE-∠BOC=90°-70°=20°,
故答案为:20;
(2)∵OD恰好平分∠BOC,∠BOC=70°,
∴∠BOD =![]() ∠BOC=35°,
∠BOC=35°,
∴∠BOE=∠BOD+∠DOE=125°,
∴∠AOE=180°-∠BOE==180°-125°=55°

练习册系列答案
相关题目
【题目】为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?