题目内容
求下列不定方程的整数解:
(1)72x+157y=1;
(2)9x+21y=144;
(3)103x-91y=5.
解:(1)由原方程得x=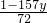 =
= ①,
①,
∵原方程的解为整数,
∴当y=-11时,x=24,是原方程的一组解,故y=72t-11,代入①式得x=24-157t(t为整数),
故原方程的解为 (t为整数).
(t为整数).
(2)由原方程得:x=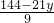 =16-2y-
=16-2y- y①,
y①,
∵方程的解整数,16-2是整数,
∴满足 是整数即可,令
是整数即可,令 y=t(t为整数),则y=3t,代入①式得,x=16-7t.
y=t(t为整数),则y=3t,代入①式得,x=16-7t.
故原方程的解为 (t为整数).
(t为整数).
(3)由原方程得x=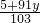 =
= ①,
①,
∵原方程的解为整数,
∴当y=9时,x=8,是原方程的一组解,
故y=103t+9,代入①式得x=91t+8(t为整数),
原方程的解为 (t为整数).
(t为整数).
分析:首先将方程做适当变形,根据解为整数确定其中一个未知数的取值,再进一步求得方程的另一个解.
点评:本题是求不定方程的整数解,先将方程做适当变形,然后列举出其中一个未知数的适合条件的所有整数值,再求出另一个未知数的值.
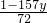 =
= ①,
①,∵原方程的解为整数,
∴当y=-11时,x=24,是原方程的一组解,故y=72t-11,代入①式得x=24-157t(t为整数),
故原方程的解为
 (t为整数).
(t为整数).(2)由原方程得:x=
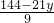 =16-2y-
=16-2y- y①,
y①,∵方程的解整数,16-2是整数,
∴满足
 是整数即可,令
是整数即可,令 y=t(t为整数),则y=3t,代入①式得,x=16-7t.
y=t(t为整数),则y=3t,代入①式得,x=16-7t.故原方程的解为
 (t为整数).
(t为整数).(3)由原方程得x=
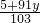 =
= ①,
①,∵原方程的解为整数,
∴当y=9时,x=8,是原方程的一组解,
故y=103t+9,代入①式得x=91t+8(t为整数),
原方程的解为
 (t为整数).
(t为整数).分析:首先将方程做适当变形,根据解为整数确定其中一个未知数的取值,再进一步求得方程的另一个解.
点评:本题是求不定方程的整数解,先将方程做适当变形,然后列举出其中一个未知数的适合条件的所有整数值,再求出另一个未知数的值.

练习册系列答案
相关题目