题目内容
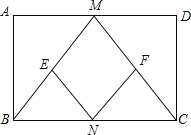
【题目】如图,在正方形ABCD中.

(1)若点E、F分别在AB、AD上,且AE=DF.试判断DE与CF的数量及位置关系,并说明理由;
(2)若P、Q、M、N是正方形ABCD各边上的点,PQ与MN相交,且PQ=MN,问PQ⊥MN成立吗?为什么?
【答案】(1)DE=CF,DE⊥CF.理由见解析;(2)MN⊥PQ成立,理由见解析;
【解析】
(1)由已知易得△DAE≌△CDF,故有DE=CF.
(2)由点N,Q分别向AB,AD作垂线,构造两直角三角形全等,由角的等量代换,易得QP⊥MN.
(1)在正方形ABCD中,AD=DC,AE=DF,∠EAD=∠FDC,
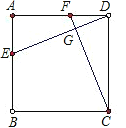
所以△EAD≌△FDC,故DE=CF,
∴∠EDA=∠FCD,
又∵∠DCF+∠DFC=90°,
∴∠ADE+∠DFC=90°,
∴∠DGF=90°
即DE⊥CF.
(2)由点N,Q分别向AB,AD作垂线,
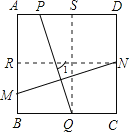
∵PQ=MN,RN=SQ,
∴△MNR≌△QPS(HL),
∴∠PQS=∠MNR,又∠1+∠PQS=90°,
所以∠1+∠MNR=90°,即MN⊥PQ.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目