题目内容
【题目】如图,∠AOB=30,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若ΔPQR周长最小,则最小周长是___________

【答案】10
【解析】
先画出图形,作PM⊥OA与OA相交于M,并将PM延长一倍到E,即ME=PM.作PN⊥OB与OB相交于N,并将PN延长一倍到F,即NF=PN.连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形.再根据线段垂直平分线的性质得出△PQR=EF,再根据三角形各角之间的关系判断出△EOF的形状即可求解.
设∠POA=θ,则∠POB=30°-θ,作PM⊥OA与OA相交于M,并将
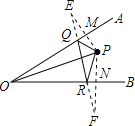
PM延长一倍到E,即ME=PM.
作PN⊥OB与OB相交于N,并将PN延长一倍到F,即NF=PN.
连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形.
∵OA是PE的垂直平分线,
∴EQ=QP;
同理,OB是PF的垂直平分线,
∴FR=RP,
∴△PQR的周长=EF.
∵OE=OF=OP=10,且∠EOF=∠EOP+∠POF=2θ+2(30°-θ)=60°,
∴△EOF是正三角形,∴EF=10,
即在保持OP=10的条件下△PQR的最小周长为10.
故答案为:10.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目