Question

【题目】如图，在中，和的角平分线相交于点，过点作交于，交于，过点作于.下列五个结论：其中正确的有（ ）

（1）；（2）；（3）点到各边的距离都相等；（4）设，若，则；（5）.（ ）

A.2个B.3个C.4个D.5个

Answer 1

【答案】B

【解析】

由在△ABC中，∠ABC和∠ACB的平分线相交于点O，根据角平分线的定义与三角形内角和定理，即可求得②∠BOC=90°+∠A正确；由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确；由角平分线定理与三角形面积的求解方法，即可求得③设OD=m，AE+AF=n，则S△AEF=mn，故③错误；E、F不可能是三角形ABC的中点，则EF不能为中位线故④正确．

解：∵在△ABC中，∠ABC和∠ACB的平分线相交于点O，
∴∠OBC=∠ABC，∠OCB=∠ACB，∠A+∠ABC+∠ACB=180°，
∴∠OBC+∠OCB=90°-∠A，
∴∠BOC=180°-（∠OBC+∠OCB）=90°+∠A；故（2）正确；
∵在△ABC中，∠ABC和∠ACB的平分线相交于点O，
∴∠OBC=∠OBE，∠OCB=∠OCF，
∵EF∥BC，
∴∠OBC=∠EOB，∠OCB=∠FOC，
∴∠EOB=∠OBE，∠FOC=∠OCF，
∴BE=OE，CF=OF，
∴EF=OE+OF=BE+CF，
故（1）正确；
过点O作OM⊥AB于M，作ON⊥BC于N，连接OA，

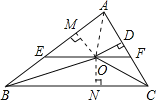
∵在△ABC中，∠ABC和∠ACB的平分线相交于点O，
∴ON=OD=OM=m，
∴S△AEF=S△AOE+S△AOF=AEOM+AFOD=OD（AE+AF）=mn；故（3）正确，故（4）错误；
∵S△EOB=BEOM，S△OCF=FCOD，
∵OM=OD，BE不一定等于CF，
∴S△EOB不一定等于SFOC．故（5）错误，
故选：B．