Question

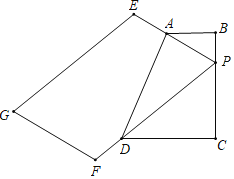
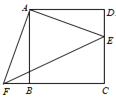
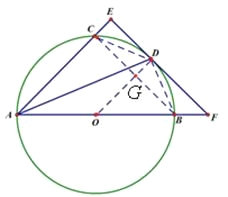
【题目】如图，AB是圆O的直径，点C、D在圆O上，且AD平分∠CAB．过点D作AC的垂线，与AC的延长线相交于E，与AB的延长线相交于点F．

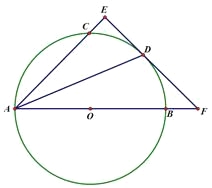
（1）求证：EF与圆O相切；

（2）若AB=6，AD=4，求EF的长．

Answer 1

【答案】（1）证明见解析；（2）EF=．

【解析】

（1）连接OD，由OA=OD可得∠OAD=∠ODA，又AD平分∠BAC从而可得∠OAD=∠CAD，从而可得∠ODA=∠CAD，继而可得OD∥AE，由EF垂直于AE，可得OD垂直于EF，从而可得EF与圆O相切；

（2）连接OD、CD、BD、BC，则CD=BD，由AB是直径，可得∠ACB=∠ADB=90°，有勾股定理可得BD=，从而CD=2，由∠ACB=∠E可得BC∥EF，由∠OAD=∠CAD，∠ADB=∠E，可得△ADE∽△ABD，从而得，可得DE=．

在Rt△CDE中，由勾股定理可得CE=，从而可得DG=．OG=3-．

在Rt△OGB中，由勾股定理可得GB=，

又由∠ACB=∠E，可得BC∥EF从而可得△OGB∽△ODF，得，从而可得DF=．所以EF=DE+DF=

=．

解：（1）连接OD，∵OA=OD，∴∠OAD=∠ODA，

又∵AD平分∠BAC，∴∠OAD=∠CAD，

∴∠ODA=∠CAD，∴OD∥AE，

又∵EF垂直于AE，

∴OD垂直于EF，

∴EF与圆O相切；

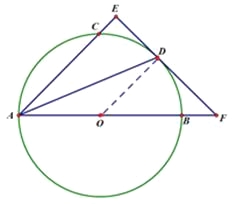
（2）连接OD、CD、BD、BC，则CD=BD，

∵AB是直径，∴∠ACB=∠ADB=90°，

又∵AB=6，AD=4，∴BD=，

∴CD=2，∵∠ACB=∠E，

∴BC∥EF，∵AD平分∠CAB，∴∠OAD=∠CAD，

又∵∠ADB=∠E，∴△ADE∽△ABD，

∴，即，∴DE=．

在Rt△CDE中，

CE=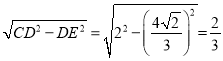

，∴DG=．OG=3-．

在Rt△OGB中，GB== =，

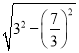∵∠ACB=∠E，∴BC∥EF．

∴△OGB∽△O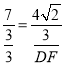DF，

∴，

∴，∴DF=．

∴EF=DE+DF=+ =．