题目内容
【题目】如图,在△ABC中,∠B=90°,AB=3,BC=2,点O在AC边上,⊙O与AB、BC分别切于点D、E,则⊙O的半径长为 . 
【答案】![]()
【解析】解:
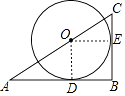
连接OE、OD,
∵⊙O与AB、BC分别切于点D、E,∠B=90°,
∴∠OEC=∠ODA=90°,∠ODB=∠B=∠OEB=90°,
∵OD=OE,
∴四边形OEBD是正方形,
∴OE=OD=DB=BE,
设OE=OD=DB=BE=R,
∵四边形OEBD是正方形,
∴OE∥AB,
∴∠COE=∠A,
∵∠OEC=∠ODA=90°,
∴△OEC∽△ADO,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:R= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】利用切线的性质定理和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目