题目内容
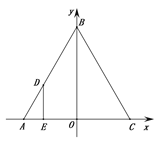
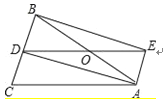
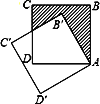
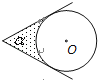
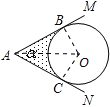
【题目】如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
A、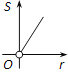 B、
B、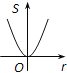 C、
C、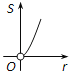 D、
D、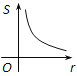
【答案】C
【解析】
试题分析:本题主要考查对切线的性质,切线长定理,三角形和扇形的面积,锐角三角函数的定义,四边形的内角和定理等知识点的理解和掌握,能综合运用性质进行计算是解此题的关键. 连接OB、OC、OA,求出∠BOC的度数,求出AB、AC的长,求出四边形OBAC和扇形OBC的面积,即可求出答案.
连接OB、OC、OA,
∵圆O切AM于B,切AN于C,
∴∠OBA=∠OCA=90°,OB=OC=r,AB=AC,
∴∠BOC=360°-90°-90°-α=(180-α)°,
∵AO平分∠MAN,
∴∠BAO=∠CAO=![]() α,
α,
AB=AC=rtan![]() α,
α,
∴阴影部分的面积是:S四边形BACO-S扇形OBC=2×![]() ×
×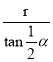 ×r-
×r-![]() =(
=( -
-![]() )r2,
)r2,
∵r>0,
∴S与r之间是二次函数关系.
故选C.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
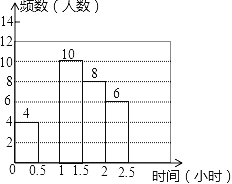
【题目】我市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出如图所示的频数分布表和频数分布直方图的一部分.
时间/时 | 频数 | 百分比 |
0≤t<0.5 | 4 | 0.1 |
0.5≤t<1 | a | 0.3 |
1≤t<1.5 | 10 | 0.25 |
1.5≤t<2 | 8 | b |
2≤t<2.5 | 6 | 0.15 |
合计 | 1 |
(1)求表中a,b的值;
(2)补全频数分布直方图;
(3)请你估算该校1400名初中学生中,约有多少名学生在1.5小时以内完成了家庭作业.