题目内容
【题目】已知y是关于x的函数,且x,y满足方程组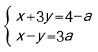 .
.
(1)求函数y的表达式;
(2)若点P的坐标为(m,0),求以P为圆心、1为半径的圆与函数y的图象有交点时,m的取值范围.
【答案】(1)y=-![]() x+
x+![]() ;(2)3-
;(2)3-![]() ≤m≤3+
≤m≤3+![]() .
.
【解析】
试题分析:本题考查直线和圆的位置关系、一次函数和坐标轴的交点、相似三角形的判定和性质以及切线的性质,题目的综合性较强,难度中等,是一道不错的中考题.
(1)把a作为已知数,分别得到x、y和a的数量关系即可求出函数y的表达式;
(2)易求点A和点B的坐标,当圆P与直线y相切时,设切点为C,则PC⊥直线y,求出此时P的横坐标即可得到函数y的图象有交点时,m的取值范围.
试题解析:(1)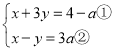 ,
,
①×3,得3x+9y=12-3a③
②+③,得4x+8y=12,即x+2y=3,
得,y=-![]() x+
x+![]() ;
;
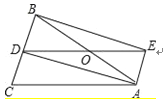
(2)当y=0时,x=3,即函数y的图象与x轴交于点A(3,0).
当x=0时,y=![]() ,即函数y的图象与y轴交于点B(0,
,即函数y的图象与y轴交于点B(0,![]() ),
),
当圆P与直线y相切时,设切点为C,则PC![]() 直线y,
直线y,
此时∠PCA=90°,
∴∠PCA=∠BOA,
且∠BAO=∠PAC,
∴△ABO∽△APC,
∴![]() ,即
,即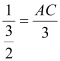 ,
,
∴AC=2,
∴PA=![]() ,
,
此时,P的横坐标为3-![]() 或3+
或3+![]() ,
,
∴当圆P与直线y有交点时,3-![]() ≤m≤3+
≤m≤3+![]() .
.

练习册系列答案
相关题目